


Next: Introduction
Wave Turbulence
"Recent developments in fluid dynamics" 5 (2004), p 225, Transworld Research Network, Kepala, India.
Yeontaek Choitex2html_wrap_inline$^*$, Yuri V. Lvovtex2html_wrap_inline$^&dagger#dagger;$, Sergey Nazarenkotex2html_wrap_inline$^*$
tex2html_wrap_inline$^*$ Mathematics Institute,
The University of Warwick,
Coventry, CV4-7AL, UK
tex2html_wrap_inline$^&dagger#dagger;$ Department of Mathematical Sciences, Rensselaer
Polytechnic Institute,
Troy, NY 12180
Abstract:
In this paper we review recent developments in the
statistical theory of weakly nonlinear dispersive waves, the subject
known as Wave Turbulence (WT). We revise WT theory using a generalisation
of the random phase approximation (RPA). This generalisation takes into
account that not only the phases but also the amplitudes of the wave
Fourier modes are random quantities and it is called the
``Random Phase and Amplitude'' approach. This approach allows to
systematically derive the kinetic equation for the energy spectrum from
the the Peierls-Brout-Prigogine (PBP) equation for the multi-mode
probability density function (PDF). The PBP equation was originally derived for the
three-wave systems and in the present paper we derive a similar equation for
the four-wave case.
Equation for the multi-mode PDF will be used to validate the
statistical assumptions about the phase and the amplitude randomness used for
WT closures. Further, the multi-mode PDF
contains a detailed statistical information, beyond spectra, and it finally
allows to study non-Gaussianity and intermittency in WT, as it will be
described in the present paper. In particular, we will show that intermittency
of stochastic nonlinear waves is related to a flux of probability in the space
of wave amplitudes.



Next: Introduction
Dr Yuri V Lvov
2007-01-23
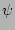 's and not
's and not 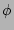 's?
's?