We have established above that the one-point statistics is at the heart of the WT theory. All one-point statistical objects can be derived from the one-point amplitude generating function,
| (79) |
First-order PDE (80) can be easily solved by the method of characteristics. Its steady state solution is
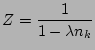 |
(82) |
| (83) |
| (87) |
| (88) |
| (89) |
At the tail of the PDF, ![]() , the solution can be represented as series
in
, the solution can be represented as series
in ![]() ,
,
Note that if the weakly nonlinearity
assumption was valid uniformly to ![]() then we had to
put
then we had to
put ![]() to ensure positivity of
to ensure positivity of ![]() and the convergence of its normalisation,
and the convergence of its normalisation,
![]() . In this case
. In this case
![]() which
is a pure Rayleigh distribution corresponding to the Gaussian wave field.
However, WT approach fails for for the
amplitudes
which
is a pure Rayleigh distribution corresponding to the Gaussian wave field.
However, WT approach fails for for the
amplitudes
![]() for which the nonlinear time is of the same order
or less than the linear wave period and, therefore, we can expect
a cut-off of
for which the nonlinear time is of the same order
or less than the linear wave period and, therefore, we can expect
a cut-off of ![]() at
at
![]() . Estimate for the value of
. Estimate for the value of
![]() can be obtained from the dynamical
equation (14) by balancing the linear and
nonlinear
terms and assuming that
if the wave amplitude at some
can be obtained from the dynamical
equation (14) by balancing the linear and
nonlinear
terms and assuming that
if the wave amplitude at some ![]() happened to be of the critical
value
happened to be of the critical
value ![]() then it will also be of similar value for a range of
then it will also be of similar value for a range of ![]() 's
of width
's
of width ![]() (i.e. the
(i.e. the ![]() -modes are strongly correlated when the amplitude is
close to critical).
This gives:
-modes are strongly correlated when the amplitude is
close to critical).
This gives:
| (91) |
Depending on the position in the wavenumber space, the flux ![]() can be
either positive or negative. As we discussed above,
can be
either positive or negative. As we discussed above, ![]() results in an
enhanced probability of large wave amplitudes with respect to the Gaussian
fields. Positive
results in an
enhanced probability of large wave amplitudes with respect to the Gaussian
fields. Positive ![]() mean depleted probability and correspond to the
wavebreaking value
mean depleted probability and correspond to the
wavebreaking value ![]() which is closer to the PDF core.
When
which is closer to the PDF core.
When ![]() gets into the core,
gets into the core,
![]() one reaches the wavenumbers
at which the breakdown is strong, i.e. of the kind considered in [32].
Consider for example the water surface gravity waves. Analysis of [32]
predicts strong breakdown in the high-
one reaches the wavenumbers
at which the breakdown is strong, i.e. of the kind considered in [32].
Consider for example the water surface gravity waves. Analysis of [32]
predicts strong breakdown in the high-![]() part of the energy cascade range.
According to our picture, these high wavenumbers correspond to the highest
positive values of
part of the energy cascade range.
According to our picture, these high wavenumbers correspond to the highest
positive values of ![]() and, therefore, the most depleted PDF tails with
respect to the Gaussian distribution. When one moves away from this region
toward lower
and, therefore, the most depleted PDF tails with
respect to the Gaussian distribution. When one moves away from this region
toward lower ![]() 's, the value of
's, the value of ![]() gets smaller and, eventually, changes the
sign leading to enhanced PDF tails at low
gets smaller and, eventually, changes the
sign leading to enhanced PDF tails at low ![]() 's.
This picture is confirmed by the direct numerical simulations of the water
surface equations reported in
[23] the results of which are shown in figure 1.
's.
This picture is confirmed by the direct numerical simulations of the water
surface equations reported in
[23] the results of which are shown in figure 1.
|
[width=.5]1.eps
|
This figure shows
that at a high ![]() the PDF tail is depleted with respect to the Rayleigh
distribution, whereas at a lower
the PDF tail is depleted with respect to the Rayleigh
distribution, whereas at a lower ![]() it is enhanced which corresponds to
intermittency at this scale.
Similar conclusion that the gravity wave turbulence is intermittent at low
rather than high wavenumbers was reached on the basis of numerical simulations
in [33].
To understand the flux reversal leading to intermittency appears in the
one-mode statistics, one has to
consider fluxes in the multi-mode phase space which will be done in the next section.
it is enhanced which corresponds to
intermittency at this scale.
Similar conclusion that the gravity wave turbulence is intermittent at low
rather than high wavenumbers was reached on the basis of numerical simulations
in [33].
To understand the flux reversal leading to intermittency appears in the
one-mode statistics, one has to
consider fluxes in the multi-mode phase space which will be done in the next section.