In this section we are going to calculate the four-wave analog of
PBP equation. These calculations are similar in spirit to
those presented in the orevious section, but with the four-wave equation
of motion (15). The calculation will be slightly
more
involved due to the frequency renormalisation, but it will be significantly
simplified by our knowledge that
(for the same reason as for three-wave case) all
![]() dependent terms will not contribute to the final result. Indeed,
any term with nonzero
dependent terms will not contribute to the final result. Indeed,
any term with nonzero ![]() would have less summations and therefore
will be of lower order. On the diagrammatic language that would mean
that all diagrams with non-zero valence can be discarded, as it was explained
in the previous section. Below, we will only keep the leading order terms
which are
would have less summations and therefore
will be of lower order. On the diagrammatic language that would mean
that all diagrams with non-zero valence can be discarded, as it was explained
in the previous section. Below, we will only keep the leading order terms
which are ![]() and wich correspond to the zero-valence diagrams.
Thus, to calculate
and wich correspond to the zero-valence diagrams.
Thus, to calculate ![]() we start with the
we start with the ![]() terms
(47),(48),(49),(50),(51) in which we put
terms
(47),(48),(49),(50),(51) in which we put ![]() and
substutute into them the values of
and
substutute into them the values of ![]() and
and
![]() from (37) and (38).
For the terms proportional to
from (37) and (38).
For the terms proportional to ![]() we have
we have
 |
|||
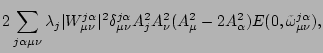 |
|||
![$\displaystyle \sum_{j\neq
k}\lambda_j\lambda_k\left[-2\vert W_{k\nu}^{j\alpha}\...
...lta_{\mu\nu}^{jk}\vert^2\delta_{\mu\nu}^{jk}A_\mu^2
\right]A_j^2 A_k^2 A_\nu^2.$](img374.png) |
(65) |