


Next: Asymptotic expansion of the
Up: Wave Turbulence "Recent developments
Previous: Weak nonlinearity expansion: three-wave
Substituting (32) in (15) we
get in the zeroth order
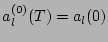 ,
and the first
iteration of (15) gives
,
and the first
iteration of (15) gives
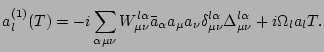 |
|
|
(31) |
Iterating one more time we get
Dr Yuri V Lvov
2007-01-23
![]() ,
and the first
iteration of (15) gives
,
and the first
iteration of (15) gives