


Next: Weak nonlinearity expansion: four-wave
Up: Wave Turbulence "Recent developments
Previous: Separation of timescales: general
Substituting the expansion (32) in (12) we
get in the zeroth order
i.e. the zeroth order term is time independent. This corresponds to
the fact that the interaction representation wave amplitudes are
constant in the linear approximation. For simplicity, we will write
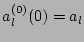 , understanding that a quantity is taken at
, understanding that a quantity is taken at 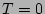 if its time argument is not mentioned explicitly.
if its time argument is not mentioned explicitly.
Here we have taken into account that
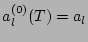 and
and
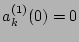 .
.
The first order is
given by
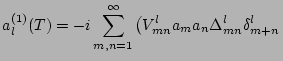 |
|
|
|
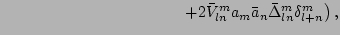 |
|
|
(30) |
Here we have taken into account that
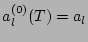 and
and
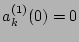 . Perform the second iteration, and integrate over
time to obtain
To calculate the second iterate, write
. Perform the second iteration, and integrate over
time to obtain
To calculate the second iterate, write
Substitute (34) into (35) and integrate over time to obtain
where we used
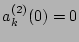 . Hereafter, we drop super-script
. Hereafter, we drop super-script 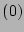 in
expressions like (36) for brevity of notations.
in
expressions like (36) for brevity of notations.



Next: Weak nonlinearity expansion: four-wave
Up: Wave Turbulence "Recent developments
Previous: Separation of timescales: general
Dr Yuri V Lvov
2007-01-23
![]() and
and
![]() .
.