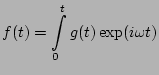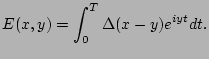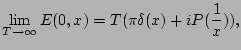Separation of timescales: general idea

When the wave amplitudes are small, the nonlinearity is weak and the wave periods, determined by the linear dynamics, are much smaller than the characteristic time at which different wave modes exchange energy. In the other words, weak nonlinearity results in a timescale separation and our goal will be to describe the slowly changing wave statistics by averaging over the fast linear oscillations. To filter out fast oscillations, we will seek seek for the solution at time $T$ such that $2 \pi / \omega \ll T \ll \tau_{nl}$. Here $\tau_{nl}$ is the characteristic time of nonlinear evolution which, as we will see later is $\sim 1/\omega \epsilon^2$ for the three-wave systems and $\sim 1/\omega \epsilon^4$ for the four-wave systems. Solution at $t=T$ can be sought at series in small small nonlinearity parameter $\epsilon$,

$$a_l(T)=a_l^{(0)}+\epsilon a_l^{(1)}+\epsilon^2 a_l^{(2)}.$$ (29)

Then we are going to iterate the equation of motion (12) or (15) to obtain $a_l^{(0)}$, $a_l^{(1)}$ and $a_l^{(2)}$ by iterations.

During this analysis the certain integrals of a type

$$f(t) = \int\limits_0^t g(t) \exp(i \omega t)$$

will play a crucial role. Following [2] we introduce

$$\Delta^l_{mn}=\int_0^T e^{i\omega^l_{mn}t}d t = \frac{({e^{i\omega^l_{mn}T}-1})}{{i \omega^l_{mn}}},$$

$$\Delta^{kl}_{mn}=\int_0^T e^{i\omega^{kl}_{mn}t}d t = \frac{({e^{i\omega^{kl}_{mn}T}-1})}{{i \omega^{kl}_{mn}}},$$

and

$$E(x,y)=\int_0^T \Delta(x-y)e^{i y t} d t .$$

We will be interested in a long time asymptotics of the above expressions, so the following properties will be useful:

$$\lim\limits_{T\to\infty}E(0,x)= T (\pi\delta(x)+iP(\frac{1}{x})),$$

and

$$\lim\limits_{T\to\infty}\vert\Delta(x)\vert^2=2\pi T\delta(x).$$