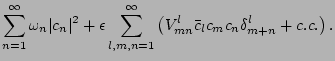Next: Four-wave case
Up: Setting the stage I:
Previous: Setting the stage I:
When
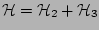 we have Hamiltonian in a form
we have Hamiltonian in a form
Equation of motion
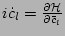 is mostly conveniently represented in the
interaction representation,
is mostly conveniently represented in the
interaction representation,
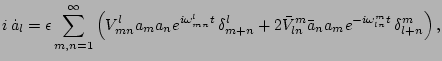 |
|
|
(10) |
where
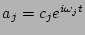 is the complex wave amplitude in the interaction
representation,
is the complex wave amplitude in the interaction
representation,
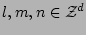 are the indices numbering the
wavevectors,
e.g.
are the indices numbering the
wavevectors,
e.g.
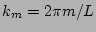 ,
, 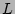 is the box side length,
is the box side length,
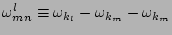 and
and
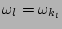 is the wave linear dispersion relation. Here,
is the wave linear dispersion relation. Here,
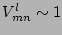 is an interaction coefficient and
is an interaction coefficient and 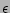 is
introduced as a formal small nonlinearity parameter.
is
introduced as a formal small nonlinearity parameter.
Dr Yuri V Lvov
2007-01-23
![]() we have Hamiltonian in a form
we have Hamiltonian in a form