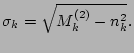Next: Separation of timescales: general
Up: Setting the stage II:
Previous: Generating functional.
Of particular interest are one-mode densities which can
be conveniently obtained using a one-amplitude
generating function
where 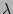 is a real parameter. Then PDF of the wave
intensities
is a real parameter. Then PDF of the wave
intensities
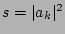 at each
at each 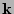 can be written as a Laplace
transform,
can be written as a Laplace
transform,
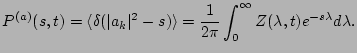 |
(26) |
For the one-point moments of the amplitude we have
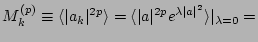 |
|
|
|
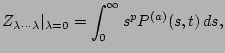 |
|
|
(27) |
where
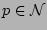 and subscript
and subscript 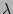 means differentiation
with respect to
means differentiation
with respect to 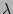
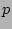 times.
times.
The first of these moments,
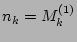 , is the waveaction spectrum.
Higher moments
, is the waveaction spectrum.
Higher moments 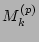 measure fluctuations of the waveaction
measure fluctuations of the waveaction 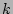 -space
distributions about their
mean values [22]. In particular the r.m.s. value of these fluctuations is
-space
distributions about their
mean values [22]. In particular the r.m.s. value of these fluctuations is
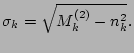 |
(28) |



Next: Separation of timescales: general
Up: Setting the stage II:
Previous: Generating functional.
Dr Yuri V Lvov
2007-01-23
![]() , is the waveaction spectrum.
Higher moments
, is the waveaction spectrum.
Higher moments ![]() measure fluctuations of the waveaction
measure fluctuations of the waveaction ![]() -space
distributions about their
mean values [22]. In particular the r.m.s. value of these fluctuations is
-space
distributions about their
mean values [22]. In particular the r.m.s. value of these fluctuations is