


Next: Wavefields with long spatial
Up: Setting the stage II:
Previous: Definition of an essentially
Importantly, RPA formulation involves independent
phase factors
 and not phases
and not phases
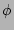 themselves. Firstly, the phases
would not be convenient because
the mean value of the phases is evolving with the rate equal to
the nonlinear frequency correction [24]. Thus one could
not say that they are ``distributed uniformly from
themselves. Firstly, the phases
would not be convenient because
the mean value of the phases is evolving with the rate equal to
the nonlinear frequency correction [24]. Thus one could
not say that they are ``distributed uniformly from 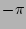 to
to 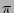 ''. Moreover the mean fluctuation
of the phase distribution is also growing and they quickly
spread beyond their initial
''. Moreover the mean fluctuation
of the phase distribution is also growing and they quickly
spread beyond their initial 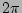 -wide interval [24].
But perhaps even more important,
-wide interval [24].
But perhaps even more important, 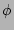 's build mutual correlations
on the nonlinear
time whereas
's build mutual correlations
on the nonlinear
time whereas 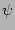 's remain independent.
Let us give a simple example
illustrating how this property is possible due
to the fact that correspondence between
's remain independent.
Let us give a simple example
illustrating how this property is possible due
to the fact that correspondence between 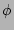 and
and 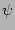 is not a bijection.
Let
is not a bijection.
Let 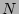 be a
random integer and let
be a
random integer and let 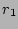 and
and  be
two independent (of
be
two independent (of 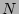 and of each other)
random numbers with uniform distribution between
and of each other)
random numbers with uniform distribution between 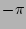 and
and
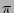 . Let
Then
and
Thus,
which means that variables
. Let
Then
and
Thus,
which means that variables 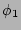 and
and
 are correlated.
On the other hand, if we introduce
then
and
which means that variables
are correlated.
On the other hand, if we introduce
then
and
which means that variables 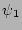 and
and
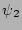 are statistically independent.
In this illustrative example it is clear
that the difference in statistical properties
between
are statistically independent.
In this illustrative example it is clear
that the difference in statistical properties
between 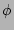 and
and 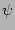 arises from the fact
that function
arises from the fact
that function
 does not have inverse
and, consequently, the information about
does not have inverse
and, consequently, the information about 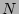 contained in
contained in 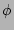 is lost in
is lost in 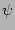 .
.
Summarising, statistics of the phase factors 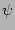 is simpler and more
convenient to use than
is simpler and more
convenient to use than 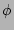 because most of the statistical objects depend only
on
because most of the statistical objects depend only
on 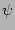 . This does not mean, however, that phases
. This does not mean, however, that phases 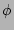 are not observable
and not interesting. Phases
are not observable
and not interesting. Phases 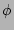 can be ``tracked'' in numerical
simulations continuously, i.e. without making jumps to
can be ``tracked'' in numerical
simulations continuously, i.e. without making jumps to 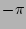 when the phase
value exceeds
when the phase
value exceeds 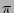 . Such continuous in
. Such continuous in 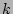 function
function 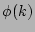 can achieve a
large range of variation in values due to the dependence of the nonlinear
rotation frequency with
can achieve a
large range of variation in values due to the dependence of the nonlinear
rotation frequency with 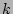 . This kind of function implies fastly fluctuating
. This kind of function implies fastly fluctuating
 which is the mechanism behind de-correlation of the
phase factors at different wavenumbers.
which is the mechanism behind de-correlation of the
phase factors at different wavenumbers.



Next: Wavefields with long spatial
Up: Setting the stage II:
Previous: Definition of an essentially
Dr Yuri V Lvov
2007-01-23
![]() is simpler and more
convenient to use than
is simpler and more
convenient to use than ![]() because most of the statistical objects depend only
on
because most of the statistical objects depend only
on ![]() . This does not mean, however, that phases
. This does not mean, however, that phases ![]() are not observable
and not interesting. Phases
are not observable
and not interesting. Phases ![]() can be ``tracked'' in numerical
simulations continuously, i.e. without making jumps to
can be ``tracked'' in numerical
simulations continuously, i.e. without making jumps to ![]() when the phase
value exceeds
when the phase
value exceeds ![]() . Such continuous in
. Such continuous in ![]() function
function ![]() can achieve a
large range of variation in values due to the dependence of the nonlinear
rotation frequency with
can achieve a
large range of variation in values due to the dependence of the nonlinear
rotation frequency with ![]() . This kind of function implies fastly fluctuating
. This kind of function implies fastly fluctuating
![]() which is the mechanism behind de-correlation of the
phase factors at different wavenumbers.
which is the mechanism behind de-correlation of the
phase factors at different wavenumbers.