next up previous
Next: Why 's and not Up: Setting the stage II: Previous: Definition of an ideal

Definition of an essentially RPA field

We will say that the field 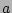$ a$ is of an ``essentially RPA'' type if:

  1. The phase factors are statistically independent and uniformly distributed variables up to $ O({\epsilon}^2)$ corrections, i.e.

    $\displaystyle {\cal P}^{(N)} \{s, \xi \} = {1 \over (2 \pi)^{N} } {\cal P}^{(N,a)} \{s \} \; [1 + O({\epsilon}^2)],$ (17)

    where

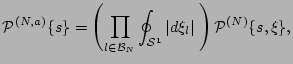    $\displaystyle {\cal P}^{(N,a)} \{s \} = \left( \prod_{ l {\cal 2 B}_N } \oint_{{\cal S}^{1} } \vert d \xi_l\vert \; \right) {\cal P}^{(N)} \{s, \xi \},$ (18)

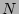    is the $ N$-mode amplitude PDF.
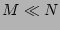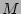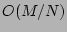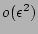  2. The amplitude variables are almost independent is a sense that for each $ M \ll N$ modes the $ M$-mode amplitude PDF is equal to the product of the one-mode PDF's up to $ O(M/N)$ and $ o({\epsilon}^2)$ corrections,

    $\displaystyle {\cal P}^{(M)}_{j_1, j_2, \dots , j_M} = P^{(a)}_{j_1} P^{(a)}_{j_2} \dots P^{(a)}_{j_M} \; [1 + O(M/N) + O({\epsilon}^2)].$ (19)


Dr Yuri V Lvov 2007-01-23