Definition of an ideal RPA field

Following the approach of [22,23], we now define a ``Random Phase and Amplitude'' (RPA) field.²We say that the field $a$ is of RPA type if it possesses the following statistical properties:

1. All amplitudes $A_l$ and their phase factors $\psi_l$ are independent random variables, i.e. their joint PDF is equal to the product of the one-mode PDF's corresponding to each individual amplitude and phase,
   $${\cal P}^{(N)} \{s, \xi \} = \prod_{ l {\cal 2 B}_N} P^{(a)}_l (s_{l}) P^{(\psi)}_l (\xi_{l})$$

2. The phase factors $\psi_l$ are uniformly distributed on the unit circle in the complex plane, i.e. for any mode $l$
   $$P^{(\psi)}_l (\xi_{l}) = 1/2\pi.$$

Note that RPA does not fix any shape of the amplitude PDF's and, therefore, can deal with strongly non-Gaussian wavefields. Such study of non-Gaussianity and intermittency of WT was presented in [22,23] and will not be repeated here. However, we will study some new objects describing statistics of the phase.

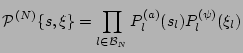
In [22,23] RPA was assumed to hold over the nonlinear time. In [24] this assumption was examined a posteriori, i.e. based on the evolution equation for the multi-point PDF obtained with RPA initial fields. Below we will describe this work. We will see that RPA fails to hold in its pure form as formulated above but it survives in the leading order so that the WT closure built using the RPA is valid. We will also see that independence of the the phase factors is quite straightforward, whereas the amplitude independence is subtle. Namely, $M$ amplitudes are independent only up to a $O(M/N)$ correction. Based on this knowledge, and leaving justification for later on in this paper, we thus reformulate RPA in a weaker form which holds over the nonlinear time and which involves $M$-mode PDF's with $M \ll N$ rather than the full $N$-mode PDF.