Let us consider a wavefield
![]() in a periodic cube of with
side
in a periodic cube of with
side ![]() and let the Fourier transform of this field be
and let the Fourier transform of this field be ![]() where
index
where
index
![]() marks the mode with wavenumber
marks the mode with wavenumber
![]() on the grid in the
on the grid in the ![]() -dimensional Fourier space. For
simplicity let us assume that there is a maximum wavenumber
-dimensional Fourier space. For
simplicity let us assume that there is a maximum wavenumber ![]() (fixed e.g. by dissipation) so that no modes with wavenumbers greater
than this maximum value can be excited. In this case, the total
number of modes is
(fixed e.g. by dissipation) so that no modes with wavenumbers greater
than this maximum value can be excited. In this case, the total
number of modes is
![]() . Correspondingly, index
. Correspondingly, index
![]() will only take values in a finite box,
will only take values in a finite box,
![]() which is centred at 0 and all sides of which are equal to
which is centred at 0 and all sides of which are equal to
![]() . To consider homogeneous turbulence, the
large box limit
. To consider homogeneous turbulence, the
large box limit
![]() will have to be taken.
1
will have to be taken.
1
Let us write the complex ![]() as
as
![]() where
where ![]() is a
real positive amplitude and
is a
real positive amplitude and ![]() is a phase factor which takes
values on
is a phase factor which takes
values on
![]() , a unit circle centred at zero in the
complex plane. Let us define the
, a unit circle centred at zero in the
complex plane. Let us define the ![]() -mode joint PDF
-mode joint PDF
![]() as the probability for the wave intensities
as the probability for the wave intensities ![]() to be in the
range
to be in the
range
![]() and for the phase factors
and for the phase factors ![]() to be on
the unit-circle segment between
to be on
the unit-circle segment between ![]() and
and
![]() for all
for all
![]() . In terms of this PDF, taking the averages will
involve integration over all the real positive
. In terms of this PDF, taking the averages will
involve integration over all the real positive ![]() 's and along all
the complex unit circles of all
's and along all
the complex unit circles of all ![]() 's,
's,
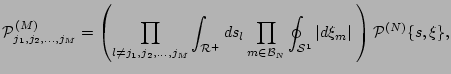 |
(16) |