


Next: Bibliography
Up: Wave Turbulence "Recent developments
Previous: Discussion.
One of the central discoveries in Wave Turbulence was the power-law
Kolmogorov-Zakharov (KZ)
spectrum,
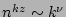 , which realise themselves in presence of the energy sources and sinks
separated by a large inertial range of scales. The exponent
, which realise themselves in presence of the energy sources and sinks
separated by a large inertial range of scales. The exponent  depends on
the
scaling properties of the interaction coefficient and the frequency. Most of the previous WT
literature
is devoted to study of KZ spectra and a good review of these works can be
found in [1]. We are not going review these studies here, but instead
we
are going to find out how adding such energy sources and sinks will this modify
the evolution equations for the statistics.
Instead of the Hamiltonian equation (1) let
us consider
depends on
the
scaling properties of the interaction coefficient and the frequency. Most of the previous WT
literature
is devoted to study of KZ spectra and a good review of these works can be
found in [1]. We are not going review these studies here, but instead
we
are going to find out how adding such energy sources and sinks will this modify
the evolution equations for the statistics.
Instead of the Hamiltonian equation (1) let
us consider
where
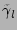 describes sources and sinks of the energy, e.g. due to
instability and viscosity respectively. Easy to see that this linear term will
not change the structure of the
describes sources and sinks of the energy, e.g. due to
instability and viscosity respectively. Easy to see that this linear term will
not change the structure of the 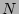 -mode PDF equation (65) but it
will lead to re-definition of the flux:
-mode PDF equation (65) but it
will lead to re-definition of the flux:
 |
(93) |
In the one-mode equations, this simply means renormalisation
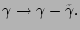 |
(94) |
Thus we arrive at a simple message that the energy sources and sinks do not
produce any ``sources'' or ``sinks'' for the flux of probability.
In the inertial range, there is no flux modification and one can easily find
 solution of (90) for the one-mode PDF,
solution of (90) for the one-mode PDF,
 |
(95) |
where  is the KZ spectrum (solving the kinetic equation in the
inertial range). However, it is easy to check by substitution that
the product of such one-mode PDF's,
is the KZ spectrum (solving the kinetic equation in the
inertial range). However, it is easy to check by substitution that
the product of such one-mode PDF's,
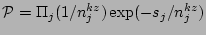 , is not an exact solution to the multi-mode equation
(65).
Thus, there have to be corrections to this expression related either to a
finite flux, an amplitude correlation or both.
, is not an exact solution to the multi-mode equation
(65).
Thus, there have to be corrections to this expression related either to a
finite flux, an amplitude correlation or both.



Next: Bibliography
Up: Wave Turbulence "Recent developments
Previous: Discussion.
Dr Yuri V Lvov
2007-01-23
![]() , which realise themselves in presence of the energy sources and sinks
separated by a large inertial range of scales. The exponent
, which realise themselves in presence of the energy sources and sinks
separated by a large inertial range of scales. The exponent ![]() depends on
the
scaling properties of the interaction coefficient and the frequency. Most of the previous WT
literature
is devoted to study of KZ spectra and a good review of these works can be
found in [1]. We are not going review these studies here, but instead
we
are going to find out how adding such energy sources and sinks will this modify
the evolution equations for the statistics.
Instead of the Hamiltonian equation (1) let
us consider
depends on
the
scaling properties of the interaction coefficient and the frequency. Most of the previous WT
literature
is devoted to study of KZ spectra and a good review of these works can be
found in [1]. We are not going review these studies here, but instead
we
are going to find out how adding such energy sources and sinks will this modify
the evolution equations for the statistics.
Instead of the Hamiltonian equation (1) let
us consider
![]() solution of (90) for the one-mode PDF,
solution of (90) for the one-mode PDF,