


Next: Five-wave kinetic equation and
Up: Five-wave interaction on the
Previous: Effective four-wave Hamiltonian
To find
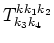 one can calculate the terms of the
order of
one can calculate the terms of the
order of 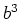 and
and 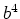 in the canonical transformation
(4.2). This very cumbersome procedure was fulfilled
by V.Krasitskii[7]. This is a kind of feat, but the resulting
formulae are so complicated that hardly can be used for any practical
purpose. In this article we offer much more simple and clear way to
in the canonical transformation
(4.2). This very cumbersome procedure was fulfilled
by V.Krasitskii[7]. This is a kind of feat, but the resulting
formulae are so complicated that hardly can be used for any practical
purpose. In this article we offer much more simple and clear way to
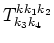 involving a Feinman's diagram technique for
the scattering matrix.
involving a Feinman's diagram technique for
the scattering matrix.
Our intermediate formulae are very complicated also, due to one-to-one
correspondense of each term in the expression to a certain graphic
picture, however all the procedure is much easy controlled. It is
very remarkable that our final formula is very simple.
First we introduce so called formal classical scattering matrix. Let
is a Hamiltonian of a some nonlinear system in a homogeneous
space. Here
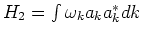 , and
, and 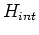 is in
general case an infinite series in power
is in
general case an infinite series in power 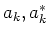
The motion equation is as usual
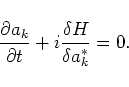 |
(5.1) |
One can change 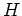 to the auxiliary Hamiltonian
to the auxiliary Hamiltonian
Now the equation (5.1) becomes linear at
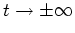 and
and
The asymptotic states 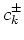 are not independent,
and actually
are not independent,
and actually
![$\hat S_{\epsilon}[c^{-}_k]$](img173.png) is a nonlinear operator
which can be presented as a series in power of
is a nonlinear operator
which can be presented as a series in power of
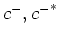 .
We will treat this series as formal one and will not care about their
convergence. A formal series which is a result of the limiting
transition
.
We will treat this series as formal one and will not care about their
convergence. A formal series which is a result of the limiting
transition
is the formal classic scattering matrix. It has the following
form
The functions 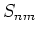 are the elements of the scattering matrix. They
are defined on the resonant manifolds
are the elements of the scattering matrix. They
are defined on the resonant manifolds
Two basic properties of the matrix elemets are important for us.
- The value of the matrix element
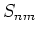 on the resonant manifold
(5.4) is invariant with respect to canonical transformation
(4.2).
on the resonant manifold
(5.4) is invariant with respect to canonical transformation
(4.2).
- There is a simple algorythm for calculation of the matrix elements.
The element
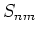 is a finite sum of terms which can be expressed
through the coefficients of the Hamiltonians
is a finite sum of terms which can be expressed
through the coefficients of the Hamiltonians
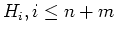 . Each term
can be marked by a certain Feinman's diagram, having no internal loops.
The rules of correspondense are described in the Appendix B.
. Each term
can be marked by a certain Feinman's diagram, having no internal loops.
The rules of correspondense are described in the Appendix B.
Actually the classical scattering matrix is nothing but the Feinman's
scattering matrix taken in the 'tree' approximation. This approximation
makes a number of terms being finite for any element.
Our idea how to find
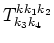 is the follow. We
calculate first nonzero elements of the scattering matrix for
the Hamiltonian (3.1) and for the Hamiltonian (4.1).
Because of these two Hamiltonians are connected by the canonical
transformation (4.2), the results must coinside.
For surface gravity waves first nontrivial matrix element is
is the follow. We
calculate first nonzero elements of the scattering matrix for
the Hamiltonian (3.1) and for the Hamiltonian (4.1).
Because of these two Hamiltonians are connected by the canonical
transformation (4.2), the results must coinside.
For surface gravity waves first nontrivial matrix element is 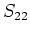 .
In terms of the Hamiltonian (4.1) it is
.
In terms of the Hamiltonian (4.1) it is
Being calculated for the Hamiltinian (3.1), this
element consist of six terms. They are presented (together with
corresponding diagrams) in the Appendix B. One can see that the result
coinside with the expression (4.3) on the resonant manifold
(1.1).
In one-dimensional case the first integral in (5.3) can be
calculated so that the first two terms in (5.3) has a form
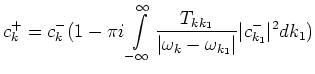 |
|
|
(5.4) |
This formula one more time stresses the fact that four-wave
nonlinear processes in one-dimensional case lead only to the trivial
scattering which does not produce ``new wave vectors''. The integral
in (5.5) diverges logarithmically. It is why our scattering matrix
is ``formal''. In reality in the one dimensional case the waves don't
became a linear indeed if 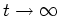 . They acquire logarithmically
growing phase (see Zakharov, Manakov [13]).
. They acquire logarithmically
growing phase (see Zakharov, Manakov [13]).
The first nontrivial element of the scattering matrix in the
one-dimensional case is
Being calculated in terms of the initial Hamiltonian (3.1)
it consists of 81 terms. Their expressions together with diagrams are
presented in the Appendix C.
In spite of complexity of the expression for
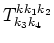 it can be enormousely simplified on the resonant manifold. We will
discuss here only the case when all
it can be enormousely simplified on the resonant manifold. We will
discuss here only the case when all 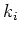 in the resonat conditions
in the resonat conditions
have the same sign.
The manifold (5.6) can be parametrised as follow
here
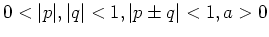 . Easy to see
that
. Easy to see
that 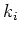 here satisfy the inequality:
here satisfy the inequality:
Plugging the parametrization (5.7) in the expression
obtained for
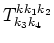 we get a sum of more than thousands
terms. Using the program for analytical calculations 'Mathematica' we
manage to simplify this expression to the following form
we get a sum of more than thousands
terms. Using the program for analytical calculations 'Mathematica' we
manage to simplify this expression to the following form
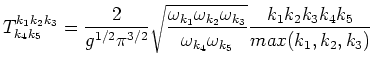 |
|
|
(5.7) |
This formula is the main result of the presented article. The fact that
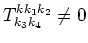 on the resonant surface means that the system
of gravity waves on a surface of deep water is nonintegrable
Hamiltonian system.
on the resonant surface means that the system
of gravity waves on a surface of deep water is nonintegrable
Hamiltonian system.



Next: Five-wave kinetic equation and
Up: Five-wave interaction on the
Previous: Effective four-wave Hamiltonian
Dr Yuri V Lvov
2007-01-17
![]() one can calculate the terms of the
order of
one can calculate the terms of the
order of ![]() and
and ![]() in the canonical transformation
(4.2). This very cumbersome procedure was fulfilled
by V.Krasitskii[7]. This is a kind of feat, but the resulting
formulae are so complicated that hardly can be used for any practical
purpose. In this article we offer much more simple and clear way to
in the canonical transformation
(4.2). This very cumbersome procedure was fulfilled
by V.Krasitskii[7]. This is a kind of feat, but the resulting
formulae are so complicated that hardly can be used for any practical
purpose. In this article we offer much more simple and clear way to
![]() involving a Feinman's diagram technique for
the scattering matrix.
involving a Feinman's diagram technique for
the scattering matrix.
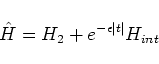
![]() is the follow. We
calculate first nonzero elements of the scattering matrix for
the Hamiltonian (3.1) and for the Hamiltonian (4.1).
Because of these two Hamiltonians are connected by the canonical
transformation (4.2), the results must coinside.
For surface gravity waves first nontrivial matrix element is
is the follow. We
calculate first nonzero elements of the scattering matrix for
the Hamiltonian (3.1) and for the Hamiltonian (4.1).
Because of these two Hamiltonians are connected by the canonical
transformation (4.2), the results must coinside.
For surface gravity waves first nontrivial matrix element is ![]() .
In terms of the Hamiltonian (4.1) it is
.
In terms of the Hamiltonian (4.1) it is
![]() it can be enormousely simplified on the resonant manifold. We will
discuss here only the case when all
it can be enormousely simplified on the resonant manifold. We will
discuss here only the case when all ![]() in the resonat conditions
in the resonat conditions