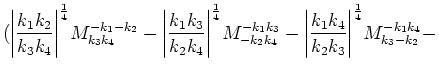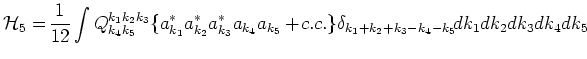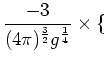Next: Effective four-wave Hamiltonian
Up: Five-wave interaction on the
Previous: Conformal canonical variables
One can introduce new variable 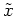 as
as
Then
Now one can expand 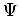 in powers of
in powers of 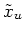 and
and 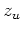
The Hamiltonian of the system is
Now
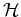 can be expanded as follow
can be expanded as follow
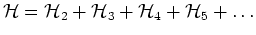 |
|
|
(3.1) |
here
Let's introduce the Fourier transform:
After simple, but a little bit tedious calculations one
can find
Here
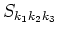 ,
,
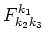 ,
,
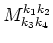 and
and
 are the functions symmetric inside of
upper and lower groups of indices. Namely
are the functions symmetric inside of
upper and lower groups of indices. Namely
The expression for
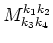 and
and
 are given in the Appendix A.
are given in the Appendix A.
It is convenient to introduce a normal complex variable 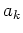
which satisfies the equation of motion
here
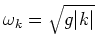 -is the dispersion law for
the gravity waves.
-is the dispersion law for
the gravity waves.
In the normal variable 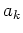 second order term in the Hamiltonian
acquires the form:
second order term in the Hamiltonian
acquires the form:
The third order term is:
Fourth order term in the Hamiltonian consists of three terms:
describing different types of the wave-wave interactions.
The term corresponding to
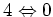 interaction has a form:
interaction has a form:
where
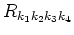 is:
is:
Term corresponding to
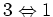 interaction has a form:
interaction has a form:
where
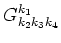 :
:
Term corresponding to
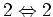 interaction has a form:
interaction has a form:
where
 :
:
Among the different terms of the fifth order we consider only the term,
corresponding to the process (1.6):
where



Next: Effective four-wave Hamiltonian
Up: Five-wave interaction on the
Previous: Conformal canonical variables
Dr Yuri V Lvov
2007-01-17
![]() as
as
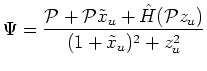
![]() in powers of
in powers of ![]() and
and ![]()
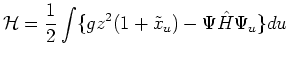
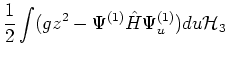
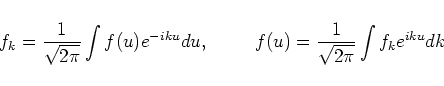
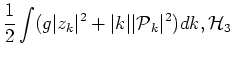
![]()
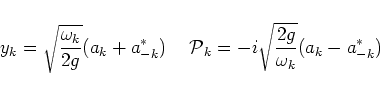
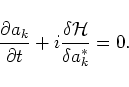
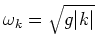 -is the dispersion law for
the gravity waves.
-is the dispersion law for
the gravity waves.
![]() second order term in the Hamiltonian
acquires the form:
second order term in the Hamiltonian
acquires the form:
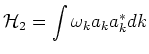
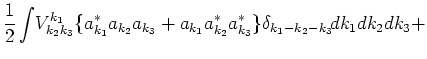
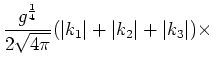
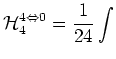
![]() is:
is:
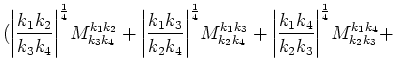
![]() interaction has a form:
interaction has a form:
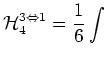
![]() :
:
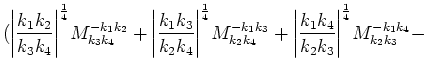
![]() interaction has a form:
interaction has a form:
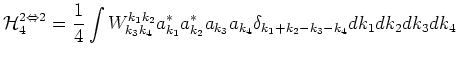
![]() :
: