


Next: Conformal canonical variables
Up: Five-wave interaction on the
Previous: Five-wave interaction on the
In this article we study interaction of gravity waves propagating in
one direction on the surface of ideal fluid of infinite depth. The
problem is of a big theoretical and practical importance. It is known
from the experiment that the distribution function of wave energy
even in the active zone of a storm is almost one-dimensional in the
energy-containing domain. Even more this is correct for the ``swell''
far away from the active zone. That is the point of common belief that the
main mechanism of wave interaction is the four-wave scattering,
satisfying the following resonant conditions
here 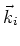 are the wave vectors of the interacting waves,
and
are the wave vectors of the interacting waves,
and
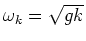 - the dispersion law. The corresponding
effective Hamiltonian has the form
- the dispersion law. The corresponding
effective Hamiltonian has the form
(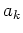 are complex amplitudes of propagating waves
[1],[2],[3]) and the corresponding kinetic
equation is
are complex amplitudes of propagating waves
[1],[2],[3]) and the corresponding kinetic
equation is
This equation is exactly equivalent (see [4])
to the Hasselmann's
equation, derived first in 1962 [5]. The equation (1.3)
is entirely adequate to the situation if 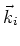 are two-dimensional
vectors. But it completely fails in the one-dimensional case.
are two-dimensional
vectors. But it completely fails in the one-dimensional case.
The equations (1.1) have in one-dimensional case two types of
solutions:
1. The trivial solutions:
Here 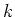 and
and 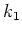 can have same or opposite signs.
can have same or opposite signs.
2. The nontrivial solutions (
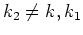 ).
).
These solutions exist only if the products 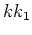 and
and
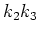 have opposite signs. They can be described analytically as
follow. Let
have opposite signs. They can be described analytically as
follow. Let 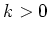 ,
, 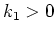 ,
, 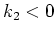 ,
, 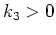 . Then
. Then
If one of the conditions (1.4) holds, the expression
is equal to zero. So, the trivial solutions do not put
any contribution to the kinetic equation (1.3). It is irrelevant
if all the wave numbers have the same sign (waves propagate in the same
direction). But even for waves propagating in the opposite directions,
four-wave interaction vanishes. As it was shown by Dyachenko and Zakharov
[6], the coefficient
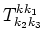 is identically equal to
zero
is identically equal to
zero
on the manifold (1.5).
This remarkable identity means that the system (1.2) is
approximately integrable and kinetic equation appears for the next
order only
Here 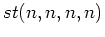 is the collision term due to five-wave
interaction, which are governed by the following resonant conditions
is the collision term due to five-wave
interaction, which are governed by the following resonant conditions
A corresponding Hamiltonian has a form
The expression 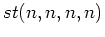 looks like that
looks like that
| |
|
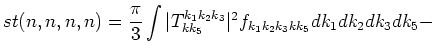 |
(1.7) |
The expression (1.7) was found by Krasitskii [7].
He also found ``in principle'' the expression for
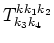 .
But his final formula is extraordinary complicated and cumbersome and hardly
can be used for any practical purpose. He used a technique of the canonical
transformation which exclude gradually the low order nonlinear terms in the
Hamiltonian.
.
But his final formula is extraordinary complicated and cumbersome and hardly
can be used for any practical purpose. He used a technique of the canonical
transformation which exclude gradually the low order nonlinear terms in the
Hamiltonian.
In this article we evaluate the coefficient
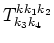 on the
resonant surface (1.6). Our final formulae are astonishingly simple.
This is one more miracle in the theory of surface waves. We also find the
Kolmogorov's solution of the stationary equation
on the
resonant surface (1.6). Our final formulae are astonishingly simple.
This is one more miracle in the theory of surface waves. We also find the
Kolmogorov's solution of the stationary equation
We will use a different technique then was used in
[1],[2],[3],[5].



Next: Conformal canonical variables
Up: Five-wave interaction on the
Previous: Five-wave interaction on the
Dr Yuri V Lvov
2007-01-17
![]() ).
).
![]() and
and
![]() have opposite signs. They can be described analytically as
follow. Let
have opposite signs. They can be described analytically as
follow. Let ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Then
. Then
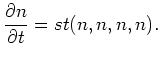
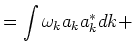
![]() on the
resonant surface (1.6). Our final formulae are astonishingly simple.
This is one more miracle in the theory of surface waves. We also find the
Kolmogorov's solution of the stationary equation
on the
resonant surface (1.6). Our final formulae are astonishingly simple.
This is one more miracle in the theory of surface waves. We also find the
Kolmogorov's solution of the stationary equation