Next: Perturbation expansion for the
Up: Five-wave interaction on the
Previous: Introduction
The basic set of equations describing a two-dimensional
potential flow of an ideal incompressible
fluid with a free surface in a gravity field fluid is
the following one:
here  - is the shape of a surface,
- is the shape of a surface,  - is a potential
function of the flow and
- is a potential
function of the flow and 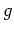 - is a gravitational constant.
As was shown by Zakharov in[1],
potential on the surface
- is a gravitational constant.
As was shown by Zakharov in[1],
potential on the surface
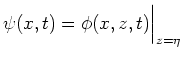 and
and 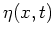 are canonically conjugated,
and their Fourier transforms satisfy the equations
are canonically conjugated,
and their Fourier transforms satisfy the equations
Here
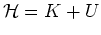 is the total energy of the fluid with the following
kinetic and potential energy terms:
is the total energy of the fluid with the following
kinetic and potential energy terms:
A Hamiltonian can be expanded in an infinite series in powers of
a characteristic wave steepness
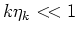 (see[,])
by using iterative procedure. All terms up to the fifth order of this series
contribute to the amplitude of five-wave interaction.
(see[,])
by using iterative procedure. All terms up to the fifth order of this series
contribute to the amplitude of five-wave interaction.
Here we prefer to do that performing first a certain canonical transformation
from the variables 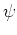 ,
, 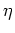 to the new canonical variables.
to the new canonical variables.
Let us perform, following Kuznetsov, Spector and Zakharov [8], a
conformal mapping of the domain 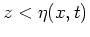 to the lower half-plane of
the complex variable
to the lower half-plane of
the complex variable
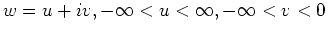 . The shape
of the surface is parametrized by two functions
. The shape
of the surface is parametrized by two functions
which are connected by the Hilbert transformation
We introduce also the complex velocity potential
On the surface ( )
)
New canonical variables can be obtained using variational
principle for the action. With old variables action is
After conformal mapping[8] it acquires the form:
Lagrangian function 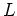 can be rewritten as
can be rewritten as
and the new canonical variables are 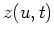 and
and
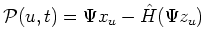 .
. 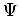 can be easily inverted as
can be easily inverted as
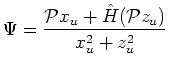 |
|
|
(2.1) |
and the Hamiltonian of the system is
where 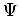 is equal to (2.1). The equations
of motion can be written in the explicit Hamiltonian form which
includes integral Hilbert's operator:
is equal to (2.1). The equations
of motion can be written in the explicit Hamiltonian form which
includes integral Hilbert's operator:



Next: Perturbation expansion for the
Up: Five-wave interaction on the
Previous: Introduction
Dr Yuri V Lvov
2007-01-17
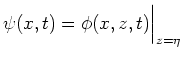 and
and 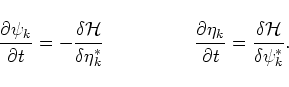
![]() is the total energy of the fluid with the following
kinetic and potential energy terms:
is the total energy of the fluid with the following
kinetic and potential energy terms:
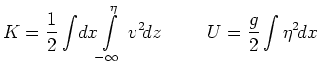
![]() (see[,])
by using iterative procedure. All terms up to the fifth order of this series
contribute to the amplitude of five-wave interaction.
(see[,])
by using iterative procedure. All terms up to the fifth order of this series
contribute to the amplitude of five-wave interaction.
![]() ,
, ![]() to the new canonical variables.
to the new canonical variables.
![]() to the lower half-plane of
the complex variable
to the lower half-plane of
the complex variable
![]() . The shape
of the surface is parametrized by two functions
. The shape
of the surface is parametrized by two functions
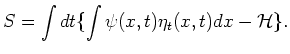
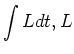
![]() can be rewritten as
can be rewritten as