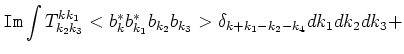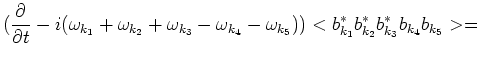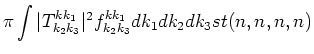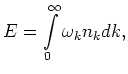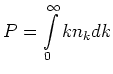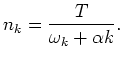Next: Appendix
Up: Five-wave interaction on the
Previous: Five-wave interaction on resonant
The matrix element
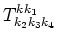 for
for
 process along with
process along with
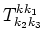 allows us to derive kinetic equation which includes four- and five-wave
interactions.
allows us to derive kinetic equation which includes four- and five-wave
interactions.
The dynamical equation for 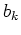 (with the Hamiltonian (4.1)) is:
(with the Hamiltonian (4.1)) is:
Introducing standard pair correlation function 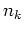
we can derive from (6.1) the equation for 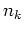 :
:
It is obvious that
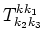 contributes to the
equation for fourth-order correlator, while
contributes to the
equation for fourth-order correlator, while
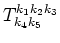 contributes to the equation for fifth-order correlator only (due to
the seventh-order correlators vanish).
Fifth-order correlation function
contributes to the equation for fifth-order correlator only (due to
the seventh-order correlators vanish).
Fifth-order correlation function
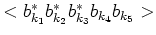 can be expressed through
the eighth-order correlator:
can be expressed through
the eighth-order correlator:
Applying random phase approximation for the eighth-order correlator
(to split it in a product of pair correlation functions) and assuming
slow variation in time for fifth-order correlator, one can
get the following expression for
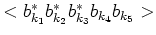 :
:
| |
|
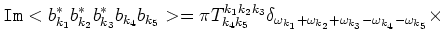 |
(6.2) |
In the (6.2) we drop the terms which are out of resonant
surface. For fourth-order correlator we have the following
equaton [15]:
| |
|
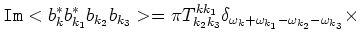 |
(6.3) |
Substituting (6.3) and (6.2) into the
equation for 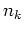 we get five-wave kinetic equation:
we get five-wave kinetic equation:
As it was shown in the Introction, In the one dimensional case
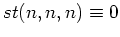 and we end up with the pure five-wave kinetic
equation:
and we end up with the pure five-wave kinetic
equation:
The equation (6.4) formally preserves two integrals of motion,
energy
and momentum
(We consider the case when all 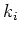 are positive).
The stationary equation
are positive).
The stationary equation
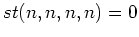 |
|
|
(6.5) |
has thermodynamic solution
Like four-wave isotropic kinetic equation, the equation
(6.4) describes direct and inverse cascades. The inverse
cascade is the cascade of energy, which is a real constant of motion
and is carried toward the small 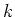 . It is described by the following
Kolmogorov solution of the equation (6.5)
. It is described by the following
Kolmogorov solution of the equation (6.5)
Here 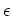 is the energy flux,
is the energy flux, 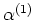 is the
Kolmogorov constant.
is the
Kolmogorov constant.
A corresponding energy spectrum is
Direct cascade is a transport of momentum towards the large wave numbers.
It is described by the Kolmogorov solution
Here 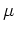 is the momentum flux,
is the momentum flux, 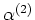 is the Kolmogorov
constant.
is the Kolmogorov
constant.
Now
Due to the direct cascade the momentum is not a real constant of motion,
it leaks permanently to the large 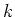 region. More detailed description
of the Kolmogorov spectra in one-dimensional case will be published
separately.
region. More detailed description
of the Kolmogorov spectra in one-dimensional case will be published
separately.
In conclusion authors express gratitude to Dr. Victor L'vov for his
valuable advises and to Alina Spectorov for preparing the diagrams.
This work is supported by the ONR Grant N00 14-92-J-1343 and Russian
Basic Research Foundation Grant N00 94-01-00898. Y.L. acknowledges
support from AFOSR Grant F49620-94-1-0144DEF.



Next: Appendix
Up: Five-wave interaction on the
Previous: Five-wave interaction on resonant
Dr Yuri V Lvov
2007-01-17
![]() (with the Hamiltonian (4.1)) is:
(with the Hamiltonian (4.1)) is: