


Next: Example: Linear Schrödinger equation
Up: The case of nearly-diagonal
Previous: Formulation and Proof of
One can also derive waveaction transport equation (6)
directly from equation of motion (25),
without obtaining first the Hamiltonian structure
(5). To do this
we define the Wigner waveaction
by using the Wigner transformation:
Then the Wigner waveaction
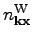 obeys the same kinetic
equation (6). The prove can be found, for example,
in [18]. To prove this formula, one calculates the
time evolution of waveaction
obeys the same kinetic
equation (6). The prove can be found, for example,
in [18]. To prove this formula, one calculates the
time evolution of waveaction
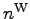 by using definition (48)
and equation of motion (25). Then one uses
transformation similar to (29,30), and expands
by using definition (48)
and equation of motion (25). Then one uses
transformation similar to (29,30), and expands
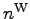 using
the smallness of
using
the smallness of 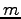 , and finally uses integration by parts to obtain
(6) - see [18] for details.
, and finally uses integration by parts to obtain
(6) - see [18] for details.
To address the question on how waveaction
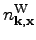 , defined through the
Wigner transformation, is related to the wave action
, defined through the
Wigner transformation, is related to the wave action
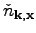 , defined
through the Gabor variables, we substitute (21) into
the definition of (48) to write
, defined
through the Gabor variables, we substitute (21) into
the definition of (48) to write
Taking into account that
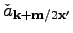 and
and
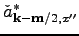 are slow functions of
are slow functions of
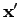 and
and
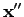 , one can neglect this slow
coordinate dependence relative to fast
, one can neglect this slow
coordinate dependence relative to fast
 dependence in the
exponent. This allows to perform
dependence in the
exponent. This allows to perform
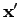 and
and
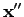 integrations to
obtain a delta-function with respect to the
integrations to
obtain a delta-function with respect to the
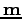 argument. Consequently we obtain that these two wave-actions,
(48) and (47) are approximately proportional to each
other:
argument. Consequently we obtain that these two wave-actions,
(48) and (47) are approximately proportional to each
other:
There are several important advantages of our method. First, it
allows to rigorously right the equation of motion for the field
variable
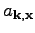 in addition to the transfer equation of
(6). In addition, our approach shows how to derive the
kinetic equation (6) to a much broader class of nonlinear
systems, those described by equation (4) with
nonzero value of
in addition to the transfer equation of
(6). In addition, our approach shows how to derive the
kinetic equation (6) to a much broader class of nonlinear
systems, those described by equation (4) with
nonzero value of
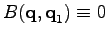 , as we show in the next section.
Lastly, Hamiltonian formulation helps significantly to establish a
wave turbulence theory, which takes into account nonlinear wave-wave
interactions.
, as we show in the next section.
Lastly, Hamiltonian formulation helps significantly to establish a
wave turbulence theory, which takes into account nonlinear wave-wave
interactions.



Next: Example: Linear Schrödinger equation
Up: The case of nearly-diagonal
Previous: Formulation and Proof of
Dr Yuri V Lvov
2008-07-08
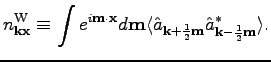
![]() , defined through the
Wigner transformation, is related to the wave action
, defined through the
Wigner transformation, is related to the wave action
![]() , defined
through the Gabor variables, we substitute (21) into
the definition of (48) to write
, defined
through the Gabor variables, we substitute (21) into
the definition of (48) to write
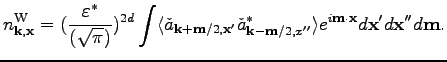
![]() in addition to the transfer equation of
(6). In addition, our approach shows how to derive the
kinetic equation (6) to a much broader class of nonlinear
systems, those described by equation (4) with
nonzero value of
in addition to the transfer equation of
(6). In addition, our approach shows how to derive the
kinetic equation (6) to a much broader class of nonlinear
systems, those described by equation (4) with
nonzero value of
![]() , as we show in the next section.
Lastly, Hamiltonian formulation helps significantly to establish a
wave turbulence theory, which takes into account nonlinear wave-wave
interactions.
, as we show in the next section.
Lastly, Hamiltonian formulation helps significantly to establish a
wave turbulence theory, which takes into account nonlinear wave-wave
interactions.