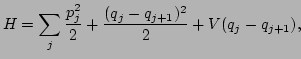 |
(1) |
In our method, the construction of the renormalized variables
![]() does not depend on a particular form or strength of the
anharmonic potential, as long as it is of the restoring type with
only the nearest neighbor interactions, as in Eq. (1).
Therefore, our approach is non-perturbative and can be applied to a
large class of systems with strong nonlinearity. However, in this
article, we will focus on the
does not depend on a particular form or strength of the
anharmonic potential, as long as it is of the restoring type with
only the nearest neighbor interactions, as in Eq. (1).
Therefore, our approach is non-perturbative and can be applied to a
large class of systems with strong nonlinearity. However, in this
article, we will focus on the ![]() -FPU chain to illustrate the
theoretical framework of the renormalized waves. We will verify that
-FPU chain to illustrate the
theoretical framework of the renormalized waves. We will verify that
![]() effectively constitute normal modes for the
effectively constitute normal modes for the ![]() -FPU
chain in thermal equilibrium by showing that (i) the theoretically
obtained renormalized linear dispersion relationship is in excellent
agreement with its dynamical manifestation in our numerical
simulation, and (ii) the equilibrium distribution of
-FPU
chain in thermal equilibrium by showing that (i) the theoretically
obtained renormalized linear dispersion relationship is in excellent
agreement with its dynamical manifestation in our numerical
simulation, and (ii) the equilibrium distribution of
![]() is
still a Rayleigh-Jeans distribution and
is
still a Rayleigh-Jeans distribution and
![]() 's are uncorrelated.
Note that similar expressions for the renormalization factor
's are uncorrelated.
Note that similar expressions for the renormalization factor ![]() have been previously discussed in the framework of an approximate
virial theorem [6] or effective long wave dynamics via
the Zwanzig-Mori projection [7]. However, in our
theory, the exact formula for the renormalization factor is derived
from a precise mathematical construction of statistical
normal modes, and is valid for all wave modes
have been previously discussed in the framework of an approximate
virial theorem [6] or effective long wave dynamics via
the Zwanzig-Mori projection [7]. However, in our
theory, the exact formula for the renormalization factor is derived
from a precise mathematical construction of statistical
normal modes, and is valid for all wave modes ![]() -- no longer
restricted to long waves.
-- no longer
restricted to long waves.
Next, we address how renormalization arises from the dynamical wave
interaction in the ![]() -FPU chain.
We will show that the
-FPU chain.
We will show that the ![]() -FPU chain can be effectively
described as a four-wave interacting Hamiltonian system of the
renormalized resonant waves
-FPU chain can be effectively
described as a four-wave interacting Hamiltonian system of the
renormalized resonant waves
![]() . We will study the resonance
structure of the
. We will study the resonance
structure of the ![]() -FPU chain and find that most of the exact
resonant interactions are trivial, i.e., the interactions
with no momentum exchange among different wave modes. In what
follows, the renormalization of the linear dispersion will be
explained as a collective effect of these trivial resonant
interactions of the renormalized waves
-FPU chain and find that most of the exact
resonant interactions are trivial, i.e., the interactions
with no momentum exchange among different wave modes. In what
follows, the renormalization of the linear dispersion will be
explained as a collective effect of these trivial resonant
interactions of the renormalized waves
![]() . We will use a
self-consistency argument to find an approximation,
. We will use a
self-consistency argument to find an approximation, ![]() , of
the renormalization factor
, of
the renormalization factor ![]() . As will be seen below, the
self-consistency argument essentially is of a mean-field type, i.e.,
the renormalization arises from the scattering of a wave by a
mean-background of waves in thermal equilibrium via trivial resonant
interactions. We note that our self-consistency, mean-field argument
is not limited to the weak nonlinearity. Very good agreement of the
renormalization factor
. As will be seen below, the
self-consistency argument essentially is of a mean-field type, i.e.,
the renormalization arises from the scattering of a wave by a
mean-background of waves in thermal equilibrium via trivial resonant
interactions. We note that our self-consistency, mean-field argument
is not limited to the weak nonlinearity. Very good agreement of the
renormalization factor ![]() and its dynamical approximation
and its dynamical approximation
![]() -- for weakly as well as strongly nonlinear waves --
confirms that the renormalization is, indeed, a direct
consequence of the trivial resonances.
-- for weakly as well as strongly nonlinear waves --
confirms that the renormalization is, indeed, a direct
consequence of the trivial resonances.
We will further study the properties of these renormalized waves by
investigating how long these waves are coherent, i.e., what their
frequency widths are. Therefore, we consider near-resonant
interactions of the renormalized waves
![]() , i.e., interactions
that occur in the vicinity of the resonance manifold, since most of
the exact resonant interactions are trivial, i.e., with no momentum
exchanges, and they, cannot effectively redistribute energy among
the wave modes.
, i.e., interactions
that occur in the vicinity of the resonance manifold, since most of
the exact resonant interactions are trivial, i.e., with no momentum
exchanges, and they, cannot effectively redistribute energy among
the wave modes.
We will demonstrate that near-resonant interactions of the
renormalized waves
![]() provide a mechanism for effective energy
exchanges among different wave modes. Taking into account the
near-resonant interactions, we will study analytically the frequency
peak broadening of the renormalized waves
provide a mechanism for effective energy
exchanges among different wave modes. Taking into account the
near-resonant interactions, we will study analytically the frequency
peak broadening of the renormalized waves
![]() by employing a
multiple time-scale, statistical averaging method. Here, we will
arrive at a theoretical prediction of the spatiotemporal spectrum
by employing a
multiple time-scale, statistical averaging method. Here, we will
arrive at a theoretical prediction of the spatiotemporal spectrum
![]() , where
, where
![]() is the Fourier transform of the
normal variable
is the Fourier transform of the
normal variable
![]() , and
, and ![]() is the frequency. The predicted
width of frequency peaks is found to be in good agreement with its
numerically measured values.
is the frequency. The predicted
width of frequency peaks is found to be in good agreement with its
numerically measured values.
In addition, for a finite ![]() -FPU chain, we will mention the
consequence, to the correlation times of waves, of the momentum
exchanges that cross over the first Brillouin zone. This process is
known as the umklapp scattering in the setting of phonon
scattering [8]. Note that, in the previous
studies [9] of the FPU chain from the wave turbulence
point of view, the effects arising from the finite nature of the
chain were not taken into account, i.e., only the limiting case of
-FPU chain, we will mention the
consequence, to the correlation times of waves, of the momentum
exchanges that cross over the first Brillouin zone. This process is
known as the umklapp scattering in the setting of phonon
scattering [8]. Note that, in the previous
studies [9] of the FPU chain from the wave turbulence
point of view, the effects arising from the finite nature of the
chain were not taken into account, i.e., only the limiting case of
![]() , where
, where ![]() is the system size, was considered.
is the system size, was considered.
The article is organized as follows. In
Section II, we discuss a chain of particles with
the nearest-neighbor nonlinear interactions. We demonstrate how to
describe a strongly nonlinear system as a system of waves that
resemble free waves in terms of the power spectrum and vanishing
correlations between waves. We show how to construct the
corresponding renormalized variables with the renormalized linear
dispersion. In Section III, we rewrite the ![]() -FPU
chain as an interacting four-wave Hamiltonian system. We study the
dynamics of the chain numerically and find excellent agreement
between the renormalized dispersion, obtained analytically and
numerically. In Section IV, we describe the
resonance manifold analytically and illustrate its controlling role
in long-time averaged dynamics using numerical simulation. In
Section V, we derive an approximation for
the renormalization factor for the linear dispersion using a
self-consistency condition. In Section VI, we study
the broadening effect of frequency peaks and predict analytically
the form of the spatiotemporal spectrum for the
-FPU
chain as an interacting four-wave Hamiltonian system. We study the
dynamics of the chain numerically and find excellent agreement
between the renormalized dispersion, obtained analytically and
numerically. In Section IV, we describe the
resonance manifold analytically and illustrate its controlling role
in long-time averaged dynamics using numerical simulation. In
Section V, we derive an approximation for
the renormalization factor for the linear dispersion using a
self-consistency condition. In Section VI, we study
the broadening effect of frequency peaks and predict analytically
the form of the spatiotemporal spectrum for the ![]() -FPU chain.
We provide the comparison of our prediction with the numerical
experiment. We present the conclusions in
Section VII.
-FPU chain.
We provide the comparison of our prediction with the numerical
experiment. We present the conclusions in
Section VII.