


Next: Self-consistency approach to frequency
Up: Interactions of renormalized waves
Previous: Numerical study of the
Dispersion relation and resonances
In order to address how the renormalized
dispersion arises from wave interactions, we study the resonance
structure of our nonlinear waves. Since the system (32) is a
Hamiltonian system with four-wave interactions, we will discuss the
properties of the resonance manifold associated with the  -FPU
system described by Eq. (32) as a first step towards the
understanding of its long time statistical behavior. We comment that
the resonance structure is one of the main objects of investigation
in wave turbulence
theory [5,22,23,24,25,26,27]. The theory of
wave turbulence focuses on the specific type of interactions, namely
resonant interactions, which dominate long time statistical
properties of the system. On the other hand, the non-resonant
interactions are usually shown to have a total vanishing average
contribution to a long time dynamics.
-FPU
system described by Eq. (32) as a first step towards the
understanding of its long time statistical behavior. We comment that
the resonance structure is one of the main objects of investigation
in wave turbulence
theory [5,22,23,24,25,26,27]. The theory of
wave turbulence focuses on the specific type of interactions, namely
resonant interactions, which dominate long time statistical
properties of the system. On the other hand, the non-resonant
interactions are usually shown to have a total vanishing average
contribution to a long time dynamics.
In analogy with quantum mechanics, where 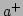 and
and 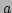 are creation
and annihilation operators, we can view
are creation
and annihilation operators, we can view
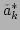 as the
outgoing wave with frequency
as the
outgoing wave with frequency
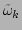 and
and
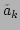 as the
incoming wave with frequency
as the
incoming wave with frequency
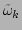 . Then, the nonlinear
term
. Then, the nonlinear
term
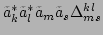 in
system (32) can be interpreted as the interaction process of
the type
in
system (32) can be interpreted as the interaction process of
the type
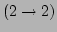 , namely, two outgoing waves with wave
numbers
, namely, two outgoing waves with wave
numbers  and
and 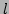 are ``created'' as a result of interaction of
the two incoming waves with wave numbers
are ``created'' as a result of interaction of
the two incoming waves with wave numbers 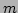 and
and 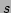 . Similarly,
. Similarly,
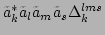 in system (32)
describes the interaction process of the type
in system (32)
describes the interaction process of the type
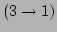 ,
that is, one outgoing wave with wave number
,
that is, one outgoing wave with wave number  is ``created'' as a
result of interaction of the three incoming waves with wave numbers
is ``created'' as a
result of interaction of the three incoming waves with wave numbers
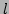 ,
, 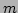 , and
, and 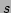 , respectively. Finally,
, respectively. Finally,
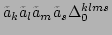 describes the interaction
process of the type
describes the interaction
process of the type
 , i.e., all four incoming
waves interact and annihilate themselves. Furthermore, the complex
conjugate terms
, i.e., all four incoming
waves interact and annihilate themselves. Furthermore, the complex
conjugate terms
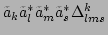 and
and
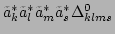 describe the
interaction processes of the type
describe the
interaction processes of the type
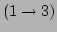 and
and
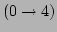 , respectively.
, respectively.
Instead of the processes with the ``momentum'' conservation given
via the usual
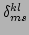 ,
,
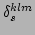 , or
, or
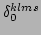 functions for an infinite discrete system, the
resonant processes of the
functions for an infinite discrete system, the
resonant processes of the  -FPU chain of a finite
size are constrained to the manifold given by
-FPU chain of a finite
size are constrained to the manifold given by
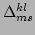 ,
,
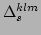 , or
, or
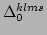 , respectively. Next, we describe
these resonant manifolds in detail. As will be pointed out in
Section VI, there is a consequence of this
finite size effect to the properties of the renormalized
waves.
, respectively. Next, we describe
these resonant manifolds in detail. As will be pointed out in
Section VI, there is a consequence of this
finite size effect to the properties of the renormalized
waves.
The resonance manifold that corresponds to the
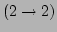 resonant processes in the discrete periodic system, therefore, is
described by
resonant processes in the discrete periodic system, therefore, is
described by
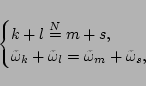 |
|
|
(37) |
where we have
introduced the notation
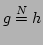 , which means that
, which means that 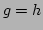 ,
, 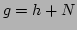 ,
or
,
or 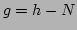 for any
for any 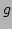 and
and 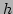 . The first equation in
system (37) is the ``momentum'' conservation condition in
the periodic wave number space. This ``momentum'' conservation comes
from
. The first equation in
system (37) is the ``momentum'' conservation condition in
the periodic wave number space. This ``momentum'' conservation comes
from
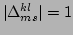 . (Note that
. (Note that
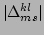 can assume only
the value of
can assume only
the value of 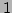 or 0.) Similarly, from
or 0.) Similarly, from
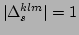 and
and
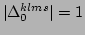 , the resonance manifolds corresponding to the
resonant processes of types
, the resonance manifolds corresponding to the
resonant processes of types
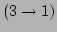 and
and
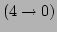 are given by
are given by
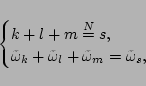 |
|
|
(38) |
and
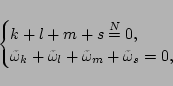 |
|
|
(39) |
respectively. For
the processes of type
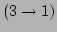 , the notation
, the notation
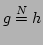 means that
means that 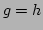 ,
, 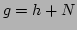 , or
, or 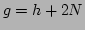 . For the
. For the
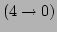 processes,
processes,
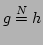 means that
means that 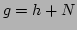 ,
, 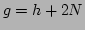 , or
, or 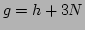 .
.
To solve system (37), we rewrite it in a continuous form
with 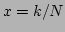 ,
, 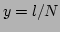 ,
, 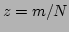 ,
, 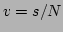 , which are
real numbers in the interval
, which are
real numbers in the interval 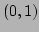 . By recalling that
. By recalling that
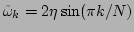 , we have
, we have
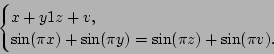 |
|
|
(40) |
Thus, any rational quartet that satisfies Eq. (40)
yields a solution for Eq. (37). There are two distinct types
of the solutions of Eq. (40). The first one corresponds
to the case
whose only solution is given
by
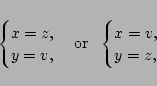 |
|
|
(41) |
i.e., these are trivial
resonances, as we mentioned above. The second type of the resonance
manifold of the
 -type interaction processes
corresponds to
-type interaction processes
corresponds to
the solution of
which can be described by the following two branches
where
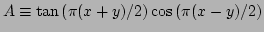 and
and 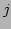 is an integer. The second type of resonances arises from the
discreteness of our model of a finite length, leading to
non-trivial resonances. For our linear dispersion here,
non-trivial resonances are only those resonances that involve wave
numbers crossing the first Brillouin zone. As mentioned above, in
the setting of the phonon physics, these non-trivial resonant
processes are also known as the umklapp scattering processes. In
Fig. 3, we plot the solution of
Eq. (40) for
is an integer. The second type of resonances arises from the
discreteness of our model of a finite length, leading to
non-trivial resonances. For our linear dispersion here,
non-trivial resonances are only those resonances that involve wave
numbers crossing the first Brillouin zone. As mentioned above, in
the setting of the phonon physics, these non-trivial resonant
processes are also known as the umklapp scattering processes. In
Fig. 3, we plot the solution of
Eq. (40) for 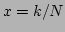 with the wave number
with the wave number 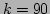 for
the system with
for
the system with 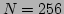 particles (the values of
particles (the values of  and
and 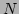 are
chosen merely for the purpose of illustration). We stress that
all the solutions of the system (40) are given
by the Eqs. (41), (42), and (43),
and that the non-trivial solutions arise only as a consequence of
discreteness of the finite chain. The curves in
Fig. 3 represent the loci of
are
chosen merely for the purpose of illustration). We stress that
all the solutions of the system (40) are given
by the Eqs. (41), (42), and (43),
and that the non-trivial solutions arise only as a consequence of
discreteness of the finite chain. The curves in
Fig. 3 represent the loci of 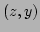 ,
parametrized by the fourth wave number
,
parametrized by the fourth wave number 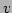 , i.e.,
, i.e.,  ,
, 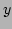 ,
, 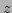 , and
, and
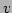 form a resonant quartet, where
form a resonant quartet, where 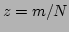 , and
, and 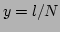 .
Note that the fourth wave number
.
Note that the fourth wave number 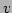 is specified by the
``momentum'' conservation, i.e., the first equation in
Eq. (40). The two straight lines in
Fig. 3 correspond to the trivial solutions, as
given by Eq. (41). The two curves (dotted and dashed)
depict the non-trivial resonances. Note that the dotted part of
non-trivial resonance curves corresponds to the
branch (42), and the dashed part corresponds to the
branch (43), respectively. An immediate question arises:
how do these resonant structures manifest themselves in the FPU
dynamics in the thermal equilibrium? By examining the
Hamiltonian (32), we notice that the resonance will control
the contribution of terms like
is specified by the
``momentum'' conservation, i.e., the first equation in
Eq. (40). The two straight lines in
Fig. 3 correspond to the trivial solutions, as
given by Eq. (41). The two curves (dotted and dashed)
depict the non-trivial resonances. Note that the dotted part of
non-trivial resonance curves corresponds to the
branch (42), and the dashed part corresponds to the
branch (43), respectively. An immediate question arises:
how do these resonant structures manifest themselves in the FPU
dynamics in the thermal equilibrium? By examining the
Hamiltonian (32), we notice that the resonance will control
the contribution of terms like
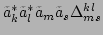 in the long time limit.
Therefore, we address the effect of resonance by computing long time
average, i.e.,
in the long time limit.
Therefore, we address the effect of resonance by computing long time
average, i.e.,
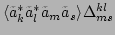 , and
comparing this average (Fig. 4) with
Fig. 3.
, and
comparing this average (Fig. 4) with
Fig. 3.
Figure 3:
The solutions of Eq. (40). The solid straight
lines correspond to the trivial resonances [solutions of
Eq. (41)]. The solutions are shown for fixed 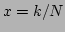 ,
,
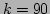 ,
, 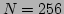 as the fourth wave number
as the fourth wave number 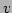 scans from
scans from 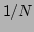 to
to 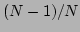 in the resonant quartet Eq. (40). The
non-trivial resonances are described by the dotted or dashed curves.
The dotted branch of the curves corresponds to the non-trivial
resonances described by Eq. (42) and and the dashed
branch corresponds to the non-trivial resonances described by
Eq. (43).
in the resonant quartet Eq. (40). The
non-trivial resonances are described by the dotted or dashed curves.
The dotted branch of the curves corresponds to the non-trivial
resonances described by Eq. (42) and and the dashed
branch corresponds to the non-trivial resonances described by
Eq. (43).
![\includegraphics[width=2.5in, height=2.5in]{resonances}](img226.png) |
Figure:
The long time average
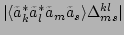 of the
of the  -FPU
system in thermal equilibrium. The parameters for the FPU chain are
-FPU
system in thermal equilibrium. The parameters for the FPU chain are
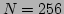 ,
, 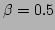 , and
, and 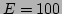 .
.
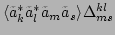 was computed for fixed
was computed for fixed
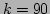 . The darker grayscale corresponds to the larger value of
. The darker grayscale corresponds to the larger value of
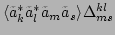 . The exact solutions of
Eq. (40), which are shown in Fig. 3,
coincide with the locations of the peaks of
. The exact solutions of
Eq. (40), which are shown in Fig. 3,
coincide with the locations of the peaks of
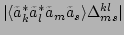 . Therefore, the
darker areas represent the near-resonance structure of the finite
. Therefore, the
darker areas represent the near-resonance structure of the finite
 -FPU chain. (The two white lines show the locations, where
-FPU chain. (The two white lines show the locations, where
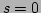 and, therefore,
and, therefore,
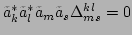 .)
[
.)
[
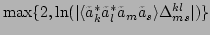 with
the corresponding grayscale is plotted for a clean presentation].
with
the corresponding grayscale is plotted for a clean presentation].
![\includegraphics[width=3in, height=2.5in]{numerical_resonance}](img230.png) |
To obtain Fig. 4, the  -FPU system was
simulated with the following parameters:
-FPU system was
simulated with the following parameters: 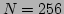 ,
, 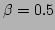 ,
,
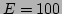 , and the averaging time window
, and the averaging time window
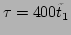 , where
, where
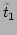 is the longest linear period, i.e.,
is the longest linear period, i.e.,
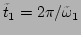 . In Fig. 4, mode
. In Fig. 4, mode
 was fixed with
was fixed with 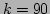 and the mode
and the mode 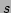 , a function of
, a function of  ,
, 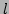 ,
and
,
and 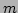 , is obtained from the constraint
, is obtained from the constraint
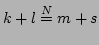 , i.e.,
, i.e.,
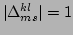 . Note that we do not impose here the condition
. Note that we do not impose here the condition
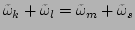 , therefore,
, therefore,
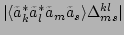 is a function of
is a function of 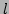 and
and 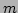 . By comparing Figs. 3 and
4, it can be observed that the locations of
the peaks of the long time average
. By comparing Figs. 3 and
4, it can be observed that the locations of
the peaks of the long time average
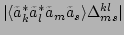 coincide with the
loci of the
coincide with the
loci of the
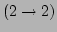 -type resonances. This observation
demonstrates that, indeed, there are nontrivial
-type resonances. This observation
demonstrates that, indeed, there are nontrivial
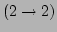 -type resonances in the finite
-type resonances in the finite  -FPU chain in thermal
equilibrium. Furthermore, it can be observed in
Fig. 4 that, in addition to the fact that the
resonances manifest themselves as the locations of the peaks of
-FPU chain in thermal
equilibrium. Furthermore, it can be observed in
Fig. 4 that, in addition to the fact that the
resonances manifest themselves as the locations of the peaks of
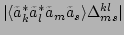 , the structure of
near-resonances is reflected in the finite width of the
peaks around the loci of the exact resonances. Note that, due to the
discrete nature of the finite
, the structure of
near-resonances is reflected in the finite width of the
peaks around the loci of the exact resonances. Note that, due to the
discrete nature of the finite  -FPU system, only those
solutions
-FPU system, only those
solutions  ,
, 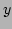 ,
, 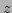 , and
, and 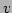 of Eq. (40), for which
of Eq. (40), for which
 ,
, 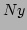 ,
, 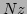 , and
, and 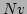 are integers, yield solutions
are integers, yield solutions  ,
, 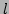 ,
,
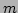 , and
, and 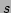 for Eq. (37). In general, the rigorous
treatment of the exact integer solutions of Eq. (37) is not
straightforward. For example, for
for Eq. (37). In general, the rigorous
treatment of the exact integer solutions of Eq. (37) is not
straightforward. For example, for 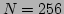 , we have the following two
exact quartets
, we have the following two
exact quartets
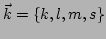 :
:
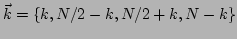 ,
,
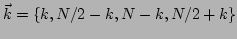 for
for
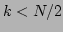 , and
, and
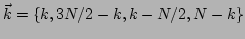 ,
,
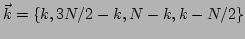 for
for 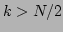 . We have verified
numerically that for
. We have verified
numerically that for 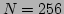 there are no other exact integer
solutions of Eq. (37). In the analysis of the resonance
width in Section VI, we will use the fact that the
number of exact non-trivial resonances [Eq. (37)] is
significantly smaller than the total number of modes.
there are no other exact integer
solutions of Eq. (37). In the analysis of the resonance
width in Section VI, we will use the fact that the
number of exact non-trivial resonances [Eq. (37)] is
significantly smaller than the total number of modes.
The broadening of the resonance peaks in
Fig. 4 suggests that, to capture the
near-resonances for characterizing long time statistical behavior of
the  -FPU system in thermal equilibrium, instead of
Eq. (37), one needs to consider the following effective
system
-FPU system in thermal equilibrium, instead of
Eq. (37), one needs to consider the following effective
system
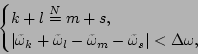 |
|
|
(44) |
where
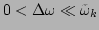 for any
for any  , and
, and
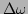 characterizes the
resonance width, which results from the near-resonace structure.
Clearly,
characterizes the
resonance width, which results from the near-resonace structure.
Clearly,
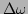 is related to the broadening of the spectral peak of
each wave
is related to the broadening of the spectral peak of
each wave
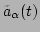 with
with
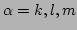 , or
, or  in the quartet, and
this broadening effect will be studied in detail in
Section VI. Note that the structure of near-resonances
is a common characteristic of many periodic discrete nonlinear wave
systems [28,29,30].
in the quartet, and
this broadening effect will be studied in detail in
Section VI. Note that the structure of near-resonances
is a common characteristic of many periodic discrete nonlinear wave
systems [28,29,30].
Further, it is easy to show that the dispersion relation of the
 -FPU chain does not allow for the occurrence of
-FPU chain does not allow for the occurrence of
 -type resonances, i.e., there are no solutions for
Eq. (38), and, therefore, all the nonlinear terms
-type resonances, i.e., there are no solutions for
Eq. (38), and, therefore, all the nonlinear terms
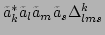 are non-resonant and their long
time average
are non-resonant and their long
time average
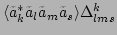 vanishes. As
for the resonances of type
vanishes. As
for the resonances of type
 , since the dispersion
relation is non-negative, one can immediately conclude that the
solution of the system (39) consists only of zero modes.
Therefore, the processes of type
, since the dispersion
relation is non-negative, one can immediately conclude that the
solution of the system (39) consists only of zero modes.
Therefore, the processes of type
 are also
non-resonant, giving rise to
are also
non-resonant, giving rise to
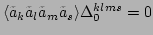 . In this article, we
will neglect the higher order effects of the near-resonances of the
types
. In this article, we
will neglect the higher order effects of the near-resonances of the
types
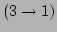 and
and
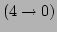 .
.
In the following sections, we will study the effects of the resonant
terms of type
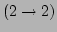 , namely, the linear dispersion
renormalization and the broadening of the frequency peaks of
, namely, the linear dispersion
renormalization and the broadening of the frequency peaks of
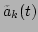 . It turns out that, the former is related to the trivial
resonance of type
. It turns out that, the former is related to the trivial
resonance of type
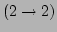 and the latter is related to
the near-resonances, as will be seen below.
and the latter is related to
the near-resonances, as will be seen below.



Next: Self-consistency approach to frequency
Up: Interactions of renormalized waves
Previous: Numerical study of the
Dr Yuri V Lvov
2007-04-11
![]() and
and ![]() are creation
and annihilation operators, we can view
are creation
and annihilation operators, we can view
![]() as the
outgoing wave with frequency
as the
outgoing wave with frequency
![]() and
and
![]() as the
incoming wave with frequency
as the
incoming wave with frequency
![]() . Then, the nonlinear
term
. Then, the nonlinear
term
![]() in
system (32) can be interpreted as the interaction process of
the type
in
system (32) can be interpreted as the interaction process of
the type
![]() , namely, two outgoing waves with wave
numbers
, namely, two outgoing waves with wave
numbers ![]() and
and ![]() are ``created'' as a result of interaction of
the two incoming waves with wave numbers
are ``created'' as a result of interaction of
the two incoming waves with wave numbers ![]() and
and ![]() . Similarly,
. Similarly,
![]() in system (32)
describes the interaction process of the type
in system (32)
describes the interaction process of the type
![]() ,
that is, one outgoing wave with wave number
,
that is, one outgoing wave with wave number ![]() is ``created'' as a
result of interaction of the three incoming waves with wave numbers
is ``created'' as a
result of interaction of the three incoming waves with wave numbers
![]() ,
, ![]() , and
, and ![]() , respectively. Finally,
, respectively. Finally,
![]() describes the interaction
process of the type
describes the interaction
process of the type
![]() , i.e., all four incoming
waves interact and annihilate themselves. Furthermore, the complex
conjugate terms
, i.e., all four incoming
waves interact and annihilate themselves. Furthermore, the complex
conjugate terms
![]() and
and
![]() describe the
interaction processes of the type
describe the
interaction processes of the type
![]() and
and
![]() , respectively.
, respectively.
![]() ,
,
![]() , or
, or
![]() functions for an infinite discrete system, the
resonant processes of the
functions for an infinite discrete system, the
resonant processes of the ![]() -FPU chain of a finite
size are constrained to the manifold given by
-FPU chain of a finite
size are constrained to the manifold given by
![]() ,
,
![]() , or
, or
![]() , respectively. Next, we describe
these resonant manifolds in detail. As will be pointed out in
Section VI, there is a consequence of this
finite size effect to the properties of the renormalized
waves.
, respectively. Next, we describe
these resonant manifolds in detail. As will be pointed out in
Section VI, there is a consequence of this
finite size effect to the properties of the renormalized
waves.
![]() resonant processes in the discrete periodic system, therefore, is
described by
resonant processes in the discrete periodic system, therefore, is
described by ![]() ,
, ![]() ,
, ![]() ,
, ![]() , which are
real numbers in the interval
, which are
real numbers in the interval ![]() . By recalling that
. By recalling that
![]() , we have
, we have ![\includegraphics[width=2.5in, height=2.5in]{resonances}](img226.png)
![\includegraphics[width=3in, height=2.5in]{numerical_resonance}](img230.png)
![]() -FPU system in thermal equilibrium, instead of
Eq. (37), one needs to consider the following effective
system
-FPU system in thermal equilibrium, instead of
Eq. (37), one needs to consider the following effective
system ![]() -FPU chain does not allow for the occurrence of
-FPU chain does not allow for the occurrence of
![]() -type resonances, i.e., there are no solutions for
Eq. (38), and, therefore, all the nonlinear terms
-type resonances, i.e., there are no solutions for
Eq. (38), and, therefore, all the nonlinear terms
![]() are non-resonant and their long
time average
are non-resonant and their long
time average
![]() vanishes. As
for the resonances of type
vanishes. As
for the resonances of type
![]() , since the dispersion
relation is non-negative, one can immediately conclude that the
solution of the system (39) consists only of zero modes.
Therefore, the processes of type
, since the dispersion
relation is non-negative, one can immediately conclude that the
solution of the system (39) consists only of zero modes.
Therefore, the processes of type
![]() are also
non-resonant, giving rise to
are also
non-resonant, giving rise to
![]() . In this article, we
will neglect the higher order effects of the near-resonances of the
types
. In this article, we
will neglect the higher order effects of the near-resonances of the
types
![]() and
and
![]() .
.
![]() , namely, the linear dispersion
renormalization and the broadening of the frequency peaks of
, namely, the linear dispersion
renormalization and the broadening of the frequency peaks of
![]() . It turns out that, the former is related to the trivial
resonance of type
. It turns out that, the former is related to the trivial
resonance of type
![]() and the latter is related to
the near-resonances, as will be seen below.
and the latter is related to
the near-resonances, as will be seen below.