


Next: Conclusions
Up: Interactions of renormalized waves
Previous: Self-consistency approach to frequency
Resonance width
Finally, we address the question of how coherent
these renormalized waves are, i.e., we study how the nonlinear
interactions of waves in thermal equilibrium broaden the
renormalized dispersion. We will obtain an analytical formula for
the spatiotemporal spectrum
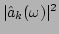 for the
for the  -FPU
chain and compare the numerically measured width of the frequency
peaks with the predicted width.
-FPU
chain and compare the numerically measured width of the frequency
peaks with the predicted width.
In the Hamiltonian (46), the nonlinear terms
corresponding to the trivial resonances have been absorbed into the
quadratic part via the effective renormalized dispersion
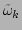 .
Therefore, the new effective Hamiltonian is
.
Therefore, the new effective Hamiltonian is
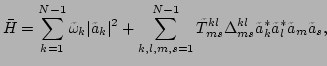 |
|
|
(54) |
where
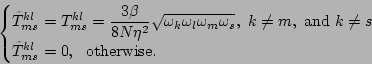 |
|
|
(55) |
The new
interaction coefficient
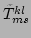 ensures that the terms that
correspond to the interactions with trivial resonances are not
doubly counted in the Hamiltonian (55) and are removed from
the quartic interaction. This new interactions in the quartic terms
include the exact non-trivial resonant and non-trivial near-resonant
as well as non-resonant interactions of the
ensures that the terms that
correspond to the interactions with trivial resonances are not
doubly counted in the Hamiltonian (55) and are removed from
the quartic interaction. This new interactions in the quartic terms
include the exact non-trivial resonant and non-trivial near-resonant
as well as non-resonant interactions of the
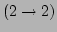 -type.
-type.
We change the variables to the interaction picture by defining the
corresponding variables 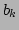 via
via
so that, the dynamics governed
by the Hamiltonian (55) takes the familiar form
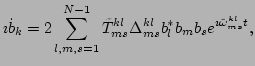 |
|
|
(56) |
where
 [23]. Without loss of
generality, we consider only the case of
[23]. Without loss of
generality, we consider only the case of 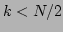 . As we have noted
before, only for a very small number of quartets does
. As we have noted
before, only for a very small number of quartets does
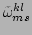 vanish exactly, i.e.,
vanish exactly, i.e.,
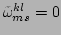 . We
separate the terms on the RHS of Eq. (57) into two kinds
-- the first kind with
. We
separate the terms on the RHS of Eq. (57) into two kinds
-- the first kind with
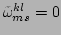 that corresponds to exact
non-trivial resonances, and the second kind that corresponds to
non-trivial near-resonances and non-resonances. Since, in the
summation, the first kind contains far fewer terms than the second
kind, and all the terms are of the same order of magnitude, we will
neglect the first kind in our analysis. Therefore, Eq. (57)
becomes
that corresponds to exact
non-trivial resonances, and the second kind that corresponds to
non-trivial near-resonances and non-resonances. Since, in the
summation, the first kind contains far fewer terms than the second
kind, and all the terms are of the same order of magnitude, we will
neglect the first kind in our analysis. Therefore, Eq. (57)
becomes
where the prime denotes the summation that
neglects the exact non-trivial resonances.
The problem of broadening of spectral peaks now becomes the study of
the frequency spectrum of the dynamical variables 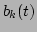 in
thermal equilibrium. This is equivalent to study the two-point
correlation in time of
in
thermal equilibrium. This is equivalent to study the two-point
correlation in time of 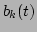
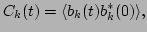 |
|
|
(58) |
where the angular brackets denote the thermal average, since,
by Wiener-Khinchin theorem, the frequency spectrum
,$](img312.png) |
|
|
(59) |
where
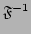 is the inverse Fourier transform in time. Under
the dynamics (58), time derivative of the two-point
correlation becomes
is the inverse Fourier transform in time. Under
the dynamics (58), time derivative of the two-point
correlation becomes
where
In order to obtain a
closed equation for 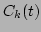 , we need to study the evolution of the
fourth order correlator
, we need to study the evolution of the
fourth order correlator
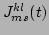 . We utilize the weak
effective nonlinearity in Eq. (55) [12] as the
small parameter in the following perturbation analysis and obtain a
closure for
. We utilize the weak
effective nonlinearity in Eq. (55) [12] as the
small parameter in the following perturbation analysis and obtain a
closure for 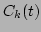 , similar to the traditional way of deriving
kinetic equation, as in [5,31]. We note that the
effective interactions of renormalized waves can be weak, as we have
shown in [12], even if the
, similar to the traditional way of deriving
kinetic equation, as in [5,31]. We note that the
effective interactions of renormalized waves can be weak, as we have
shown in [12], even if the  -FPU chain is in a
strongly nonlinear regime. Our perturbation analysis is a multiple
time-scale, statistical averaging method. Under the near-Gaussian
assumption, which is applicable for the weakly nonlinear wave fields
in thermal equilibrium, for the four-point correlator, we obtain
-FPU chain is in a
strongly nonlinear regime. Our perturbation analysis is a multiple
time-scale, statistical averaging method. Under the near-Gaussian
assumption, which is applicable for the weakly nonlinear wave fields
in thermal equilibrium, for the four-point correlator, we obtain
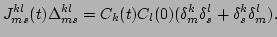 |
|
|
(61) |
Combining Eqs. (56) and (62), we find that the
right-hand side of Eq. (61) vanishes because
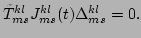 |
|
|
(62) |
Therefore, we
need to proceed to the higher order contribution of
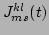 . Taking its time derivative yields
. Taking its time derivative yields
Considering the right-hand side of Eq. (64) term by
term, for the first term, we have
We can use the near-Gaussian assumption to split the correlator
of the sixth order in Eq. (65) into the product of three
correlators of the second order, namely,
where we have used that
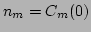 . Then, Eq. (65)
becomes
. Then, Eq. (65)
becomes
| |
|
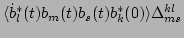 |
|
| |
|
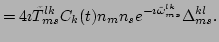 |
(65) |
Similarly, for the
remaining two terms in Eq. (64), we have
| |
|
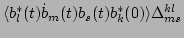 |
|
| |
|
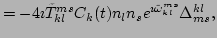 |
(66) |
and
| |
|
 |
|
| |
|
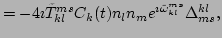 |
(67) |
respectively.
Combining Eqs. (66), (67), and (68) with
Eq. (64), we obtain
Equation (69) can be solved for
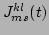 under the
assumption that the term
under the
assumption that the term
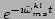 oscillates much
faster than
oscillates much
faster than 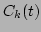 . We numerically verify [Fig. 9
below] the validity of this assumption of time-scale separation.
Under this approximation, the solution of Eq. (69) becomes
. We numerically verify [Fig. 9
below] the validity of this assumption of time-scale separation.
Under this approximation, the solution of Eq. (69) becomes
Plugging
Eq. (70) into Eq. (61), we obtain the following
equation for 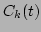
Since in the
thermal equilibrium 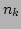 is known, i.e.,
is known, i.e.,
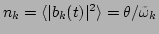 [Eq. (26)], Eq. (71)
becomes a closed equation for
[Eq. (26)], Eq. (71)
becomes a closed equation for 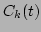 . The solution of
Eq. (71) yields the autocorrelation function
. The solution of
Eq. (71) yields the autocorrelation function 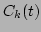
Using
this observation, together with Eq. (56), finally, we obtain
for the thermalized  -FPU chain
-FPU chain
Equation (73) gives a direct way of computing the
correlation function of the renormalized waves
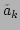 , which, in
turn, allows us to predict the spatiotemporal spectrum
, which, in
turn, allows us to predict the spatiotemporal spectrum
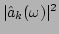 . In Fig. 6(a), we plot the
analytical prediction (via Eq. (73)) of the spatiotemporal
spectrum
. In Fig. 6(a), we plot the
analytical prediction (via Eq. (73)) of the spatiotemporal
spectrum
$](img352.png) .
By comparing this plot with the one presented in
Fig. 6(b), in which the corresponding numerically
measured spatiotemporal spectrum is shown, it can be seen that the
analytical prediction of the frequency spectrum via Eq. (73) is
in good qualitative agreement with the numerically measured one.
However, to obtain a more detailed comparison of the analytical
prediction with the numerical observation, we show, in
Fig. 7, the numerical frequency spectra of selected wave
modes with the corresponding analytical predictions. It can be
clearly observed that the agreement is rather good.
.
By comparing this plot with the one presented in
Fig. 6(b), in which the corresponding numerically
measured spatiotemporal spectrum is shown, it can be seen that the
analytical prediction of the frequency spectrum via Eq. (73) is
in good qualitative agreement with the numerically measured one.
However, to obtain a more detailed comparison of the analytical
prediction with the numerical observation, we show, in
Fig. 7, the numerical frequency spectra of selected wave
modes with the corresponding analytical predictions. It can be
clearly observed that the agreement is rather good.
Figure:
(a) Plot of the analytical prediction for the
spatiotemporal spectrum
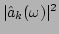 via Eq. (73). (b) Plot
of the numerically measured spatiotemporal spectrum
via Eq. (73). (b) Plot
of the numerically measured spatiotemporal spectrum
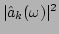 .
The parameters in both plots were
.
The parameters in both plots were 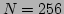 ,
,
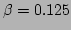 ,
, 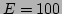 and
and 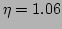 ,
,
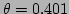 .
. 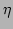 and
and 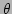 were computed
analytically via Gibbs measure. The darker gray scale correspond to
larger values of
were computed
analytically via Gibbs measure. The darker gray scale correspond to
larger values of
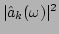 in
in  -
- space.
[
space.
[
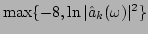 is plotted for clear
presentation].
is plotted for clear
presentation].
![\includegraphics[width=3in, height=2.5in]{awk_both}](img353.png) |
Figure:
Temporal frequency spectrum
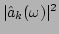 for
for  (left peak) and
(left peak) and  (right peak). The numerical spectrum is shown
with pluses and the analytical prediction [via Eq. (73)] is
shown with solid line. The parameters were
(right peak). The numerical spectrum is shown
with pluses and the analytical prediction [via Eq. (73)] is
shown with solid line. The parameters were 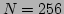 ,
,
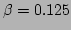 ,
,
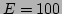 .
.
![\includegraphics[width=3in, height=2.5in]{aw}](img354.png) |
One of the important characteristics of the frequency spectrum is
the width of the spectrum. We compute the width 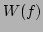 of the
spectrum
of the
spectrum
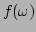 by
by
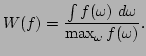 |
|
|
(73) |
In Fig. 8, we compare the width, as a function
of the wave number  , of the frequency peaks from the numerical
observation with that obtained from the analytical predictions. We
observe that, for weak nonlinearity (
, of the frequency peaks from the numerical
observation with that obtained from the analytical predictions. We
observe that, for weak nonlinearity (
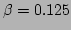 ), the analytical
prediction and the numerical observation are in excellent agreement.
In the weakly nonlinear regime, this agreement can be attributed to
the validity of (i) the near-Gaussian assumption, and (ii) the
separation between the linear dispersion time scale and the time
scale of the correlation
), the analytical
prediction and the numerical observation are in excellent agreement.
In the weakly nonlinear regime, this agreement can be attributed to
the validity of (i) the near-Gaussian assumption, and (ii) the
separation between the linear dispersion time scale and the time
scale of the correlation 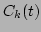 . This separation was used in
deriving the analytical prediction [Eq. (73)]. However, when
the nonlinearity becomes larger (
. This separation was used in
deriving the analytical prediction [Eq. (73)]. However, when
the nonlinearity becomes larger (
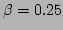 and
and 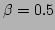 ), the
discrepancy between the numerical measurements and the analytical
prediction increases, as can be seen in Fig. 8.
Nevertheless, it is important to emphasize that, even for very
strong nonlinearity, our prediction is still qualitatively valid, as
seen in Fig. 8. In order to find out the effect of
the umklapp scattering due to the finite size of the chain, we also
computed the correlation [Eq. (73)] with the ``conventional''
), the
discrepancy between the numerical measurements and the analytical
prediction increases, as can be seen in Fig. 8.
Nevertheless, it is important to emphasize that, even for very
strong nonlinearity, our prediction is still qualitatively valid, as
seen in Fig. 8. In order to find out the effect of
the umklapp scattering due to the finite size of the chain, we also
computed the correlation [Eq. (73)] with the ``conventional''
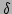 -function
-function
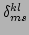 (i.e., without taking into
account the umklapp processes) instead of our ``periodic'' delta
function
(i.e., without taking into
account the umklapp processes) instead of our ``periodic'' delta
function
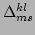 . It turns out that the correlation time is
approximately
. It turns out that the correlation time is
approximately 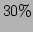 larger if it is computed without umklapp
processes taken into account for the case
larger if it is computed without umklapp
processes taken into account for the case 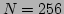 ,
, 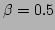 ,
,
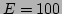 . It demonstrates that the influence of the non-trivial
umklapp resonances is important and should be considered when one
describes the dynamics of the finite length chain of particles.
. It demonstrates that the influence of the non-trivial
umklapp resonances is important and should be considered when one
describes the dynamics of the finite length chain of particles.
Figure:
Frequency peak width
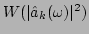 as a function of
the wave number
as a function of
the wave number  . The analytical prediction via Eq. (73) is
shown with a dashed line and the numerical observation is plotted
with solid circles. The parameters were
. The analytical prediction via Eq. (73) is
shown with a dashed line and the numerical observation is plotted
with solid circles. The parameters were 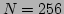 ,
, 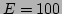 . The upper
thick lines correspond to
. The upper
thick lines correspond to 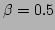 , the middle fine lines
correspond to
, the middle fine lines
correspond to
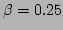 , and the lower solid circle and dashed
line (almost overlap) correspond to
, and the lower solid circle and dashed
line (almost overlap) correspond to
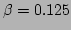 .
.
![\includegraphics[width=3in, height=2.5in]{widths}](img360.png) |
Finally, in Fig. 9, we verify the time scale separation
assumption used in our derivation, i.e., the correlation time of the
wave mode  is sufficiently larger than the corresponding linear
dispersion period
is sufficiently larger than the corresponding linear
dispersion period
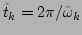 . In the case of small
nonlinearity (
. In the case of small
nonlinearity (
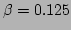 ), the two-point correlation changes over
much slower time scale than the corresponding linear oscillations
-- the correlation time is nearly two orders of magnitude larger than the corresponding linear oscillations for weak nonlinearity
), the two-point correlation changes over
much slower time scale than the corresponding linear oscillations
-- the correlation time is nearly two orders of magnitude larger than the corresponding linear oscillations for weak nonlinearity
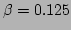 , and
nearly one order of magnitude larger than the corresponding linear
oscillations for stronger nonlinearity
, and
nearly one order of magnitude larger than the corresponding linear
oscillations for stronger nonlinearity
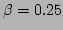 and
and 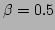 .
This demonstrates that the renormalized waves have long lifetimes,
i.e., they are coherent over time-scales that are much longer than
their oscillation time-scales.
.
This demonstrates that the renormalized waves have long lifetimes,
i.e., they are coherent over time-scales that are much longer than
their oscillation time-scales.
Figure 9:
Ratio, as a function of  , of the correlation time
, of the correlation time
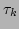 of the mode
of the mode  to the corresponding linear period
to the corresponding linear period
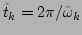 . Circles, squares, and diamonds represent the
analytical prediction for
. Circles, squares, and diamonds represent the
analytical prediction for 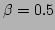 ,
,
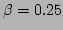 , and
, and
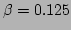 respectively. Stars, pentagrams, and triangles
correspond to the numerical observation for
respectively. Stars, pentagrams, and triangles
correspond to the numerical observation for 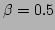 ,
,
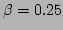 , and
, and
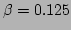 respectively. The parameters were
respectively. The parameters were
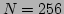 ,
, 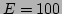 . The ratio is sufficiently large for all wave
numbers
. The ratio is sufficiently large for all wave
numbers  even for relatively large
even for relatively large 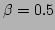 , which validates
the time-scale separation assumption used in deriving Eq. (70).
The comparison also suggests that for smaller
, which validates
the time-scale separation assumption used in deriving Eq. (70).
The comparison also suggests that for smaller  the analytical
prediction should be closer to the numerical observation, as is
confirmed in Fig. 8.
the analytical
prediction should be closer to the numerical observation, as is
confirmed in Fig. 8.
![\includegraphics[width=3in, height=2.5in]{awk_corr}](img362.png) |



Next: Conclusions
Up: Interactions of renormalized waves
Previous: Self-consistency approach to frequency
Dr Yuri V Lvov
2007-04-11
![]() .
Therefore, the new effective Hamiltonian is
.
Therefore, the new effective Hamiltonian is ![]() via
via ![]() in
thermal equilibrium. This is equivalent to study the two-point
correlation in time of
in
thermal equilibrium. This is equivalent to study the two-point
correlation in time of ![]()
![\includegraphics[width=3in, height=2.5in]{awk_both}](img353.png)
![\includegraphics[width=3in, height=2.5in]{aw}](img354.png)
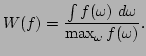
![\includegraphics[width=3in, height=2.5in]{widths}](img360.png)
![\includegraphics[width=3in, height=2.5in]{awk_corr}](img362.png)