


Next: Numerical study of the
Up: Interactions of renormalized waves
Previous: Introduction
Renormalized waves
Consider a chain of particles coupled via
nonlinear springs. Suppose the total number of particles is 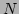 and
the momentum and displacement from the equilibrium position of the
and
the momentum and displacement from the equilibrium position of the
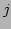 -th particle are
-th particle are 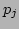 and
and 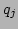 , respectively. If only the
nearest-neighbor interactions are present, then the chain can be
described by the Hamiltonian
, respectively. If only the
nearest-neighbor interactions are present, then the chain can be
described by the Hamiltonian
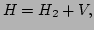 |
|
|
(6) |
where
the quadratic part of the Hamiltonian takes the form
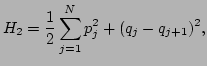 |
|
|
(7) |
and the anharmonic potential 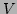 is the function of the relative
displacement
is the function of the relative
displacement
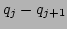 . Here periodic boundary conditions
. Here periodic boundary conditions
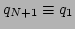 and
and
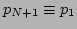 are imposed. Since the
total momentum of the system is conserved, it can be set to zero.
are imposed. Since the
total momentum of the system is conserved, it can be set to zero.
In order to study the distribution of energy among the wave modes,
we transform the Hamiltonian to the Fourier variables 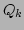 ,
, 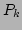 via
via
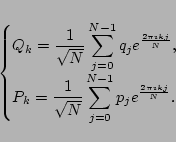 |
|
|
(8) |
This transformation is
canonical [10,11] and the Hamiltonian (6)
becomes
where
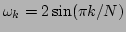 is the linear dispersion relation.
Note that, throughout the paper, for the simplicity of notation, we
denote the periodic wave number space by the set of integers in the
range
is the linear dispersion relation.
Note that, throughout the paper, for the simplicity of notation, we
denote the periodic wave number space by the set of integers in the
range ![$ [0,N-1]$](img77.png) , i.e., we drop the conventional factor,
, i.e., we drop the conventional factor, 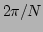 .
The zeroth mode vanishes due to the fact that the total momentum is
zero.
.
The zeroth mode vanishes due to the fact that the total momentum is
zero.
If the system (9) is in thermal equilibrium, then the
canonical Gibbs measure, with the corresponding partition function
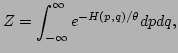 |
|
|
(10) |
with the temperature 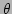 , can be used to describe the
statistical behavior of the system. We consider the systems with the
anharmonic potential of the restoring type, i.e., the potential for
which the integral in Eq. (10) converges. It can be easily
shown that for system (9) the average kinetic energy
, can be used to describe the
statistical behavior of the system. We consider the systems with the
anharmonic potential of the restoring type, i.e., the potential for
which the integral in Eq. (10) converges. It can be easily
shown that for system (9) the average kinetic energy
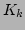 of each mode is independent of the wave number
of each mode is independent of the wave number
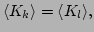 |
|
|
(11) |
where  and
and 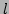 are wave
numbers,
are wave
numbers,
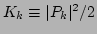 , and
, and
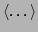 denotes averaging
over the Gibbs measure. Similarly, the average quadratic potential
denotes averaging
over the Gibbs measure. Similarly, the average quadratic potential
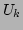 of each mode is independent of the wave number
of each mode is independent of the wave number
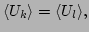 |
|
|
(12) |
where
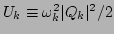 .
.
If the nonlinear interactions are weak, then it is convenient to
further transform the Hamiltonian (9) to the complex
normal variables defined by Eq. (2). This transformation
is canonical, i.e., the dynamical equation of motion becomes
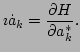 |
|
|
(13) |
In terms of these normal variables, the
Hamiltonian (9) takes the form (3). For the
system of noninteracting waves, i.e.,
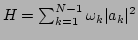 , we obtain a standard virial theorem
in the form
, we obtain a standard virial theorem
in the form
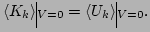 |
|
|
(14) |
As a consequence of this virial
theorem, we have the properties of free waves, which were already
mentioned above [Eqs. (4) and (5)], i.e.,
for all wave numbers  and
and 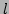 . Note that
equation (15) gives the classical Rayleigh-Jeans distribution
for the power spectrum of free waves [5]
. Note that
equation (15) gives the classical Rayleigh-Jeans distribution
for the power spectrum of free waves [5]
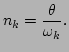 |
|
|
(17) |
However, if the nonlinearity is
present, the waves 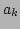 and
and 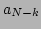 become correlated, i.e.,
become correlated, i.e.,
 |
|
|
(18) |
since the property (14) is no longer
valid.
As we mentioned before, a complete set of new renormalized variables
 can be constructed, so that the strongly nonlinear system
can be viewed as a system of ``free'' waves in the sense of
vanishing correlations and the power spectrum, i.e., the new
variables
can be constructed, so that the strongly nonlinear system
can be viewed as a system of ``free'' waves in the sense of
vanishing correlations and the power spectrum, i.e., the new
variables
 satisfy the properties of free waves given in
Eqs. (15) and (16). Next, we show how to construct
these renormalized variables
satisfy the properties of free waves given in
Eqs. (15) and (16). Next, we show how to construct
these renormalized variables
 .
.
Consider the generalization of the transformation (2),
namely, the transformation from the Fourier variables 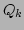 and
and
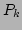 to the renormalized variables
to the renormalized variables
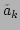 by
by
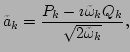 |
|
|
(19) |
where
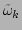 is an arbitrary function with the only restrictions
is an arbitrary function with the only restrictions
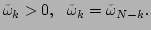 |
|
|
(20) |
One can show that,
these restrictions (20) provide a necessary and
sufficient condition for the transformation (19) to be
canonical. For the renormalized waves
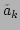 , we can compute
, we can compute
Since we have the freedom of choosing any
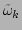 (with the
only restrictions (20)), we can chose
(with the
only restrictions (20)), we can chose
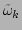 such that
such that
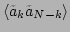 vanishes. Thus, the renormalized variables
vanishes. Thus, the renormalized variables
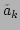 for a strongly nonlinear system will behave like the bare
variables
for a strongly nonlinear system will behave like the bare
variables 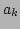 for a noninteracting system in terms of vanishing
correlations between waves. Therefore, we determine
for a noninteracting system in terms of vanishing
correlations between waves. Therefore, we determine
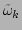 via
via
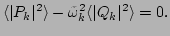 |
|
|
(23) |
Note that
the requirement (23) has the form of the virial theorem
for the free waves but with the renormalized linear dispersion
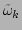 . We rewrite Eq. (23) in terms of the kinetic and
quadratic potential parts of the energy of the mode
. We rewrite Eq. (23) in terms of the kinetic and
quadratic potential parts of the energy of the mode  as
as
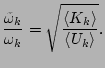 |
|
|
(24) |
The in Eqs. (11)
and (12) leads to the  independence of the right-hand
side of Eq. (24). This allows us to define the
renormalization factor
independence of the right-hand
side of Eq. (24). This allows us to define the
renormalization factor 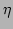 for all
for all  's by
's by
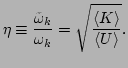 |
|
|
(25) |
for dispersion 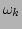 . Here
. Here
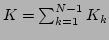 and
and
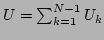 are the kinetic
and the quadratic potential parts of the total energy of the
system (9), respectively. Note that the way of
constructing the renormalized variables
are the kinetic
and the quadratic potential parts of the total energy of the
system (9), respectively. Note that the way of
constructing the renormalized variables
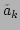 via the precise
requirement of vanishing correlations between waves yields the exact
expression for the renormalization factor, which is valid for all
wave numbers
via the precise
requirement of vanishing correlations between waves yields the exact
expression for the renormalization factor, which is valid for all
wave numbers  and any strength of nonlinearity. The independence
of
and any strength of nonlinearity. The independence
of 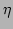 of the wave number
of the wave number  is a consequence of the Gibbs
measure. This
is a consequence of the Gibbs
measure. This  independence phenomenon has been observed in
previous numerical experiments [12,6]. We will
elaborate on this point in the results of the numerical experiment
presented in Section III.
independence phenomenon has been observed in
previous numerical experiments [12,6]. We will
elaborate on this point in the results of the numerical experiment
presented in Section III.
The immediate consequence of the fact that 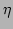 is independent of
is independent of
 is that the power spectrum of the renormalized waves possesses
the precise Rayleigh-Jeans distribution, i.e.,
is that the power spectrum of the renormalized waves possesses
the precise Rayleigh-Jeans distribution, i.e.,
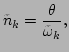 |
|
|
(26) |
from Eq. (21),
where
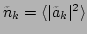 . Combining Eqs. (2)
and (19), we find the relation between the ``bare'' waves
. Combining Eqs. (2)
and (19), we find the relation between the ``bare'' waves
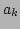 and the renormalized waves
and the renormalized waves
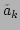 to be
to be
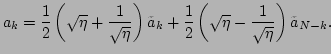 |
|
|
(27) |
Using Eq. (27), we obtain the following form of the
power spectrum for the bare waves 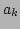
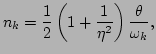 |
|
|
(28) |
which is a modified Rayleigh-Jeans distribution due to the
renormalization factor
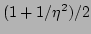 . Naturally, if the
nonlinearity becomes weak, we have
. Naturally, if the
nonlinearity becomes weak, we have
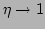 , and,
therefore, all the variables and parameters with tildes reduce to
the corresponding ``bare'' quantities, in particular,
, and,
therefore, all the variables and parameters with tildes reduce to
the corresponding ``bare'' quantities, in particular,
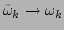 ,
,
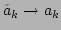 ,
,
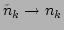 . It is interesting to point out that,
even in a strongly nonlinear regime, the ``free-wave'' form of the
Rayleigh-Jeans distribution is satisfied
exactly [Eq. (26)] by the renormalized waves. Thus,
we have demonstrated that even in the presence of strong
nonlinearity, the system in thermal equilibrium can still be viewed
statistically as a system of ``free'' waves in the sense of
vanishing correlations between waves and the power spectrum.
. It is interesting to point out that,
even in a strongly nonlinear regime, the ``free-wave'' form of the
Rayleigh-Jeans distribution is satisfied
exactly [Eq. (26)] by the renormalized waves. Thus,
we have demonstrated that even in the presence of strong
nonlinearity, the system in thermal equilibrium can still be viewed
statistically as a system of ``free'' waves in the sense of
vanishing correlations between waves and the power spectrum.
Note that, in the derivation of the formula for the renormalization
factor [Eq. (25)], we only assumed the nearest-neighbor
interactions, i.e., the potential is the function of
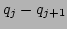 .
One of the well-known examples of such a system is the
.
One of the well-known examples of such a system is the  -FPU
chain, where only the forth order nonlinear term in
-FPU
chain, where only the forth order nonlinear term in 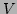 is present.
In the remainder of the article, we will focus on the
is present.
In the remainder of the article, we will focus on the  -FPU to
illustrate the framework of the renormalized waves
-FPU to
illustrate the framework of the renormalized waves
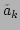 .
.



Next: Numerical study of the
Up: Interactions of renormalized waves
Previous: Introduction
Dr Yuri V Lvov
2007-04-11
![]() ,
, ![]() via
via ![]() can be constructed, so that the strongly nonlinear system
can be viewed as a system of ``free'' waves in the sense of
vanishing correlations and the power spectrum, i.e., the new
variables
can be constructed, so that the strongly nonlinear system
can be viewed as a system of ``free'' waves in the sense of
vanishing correlations and the power spectrum, i.e., the new
variables
![]() satisfy the properties of free waves given in
Eqs. (15) and (16). Next, we show how to construct
these renormalized variables
satisfy the properties of free waves given in
Eqs. (15) and (16). Next, we show how to construct
these renormalized variables
![]() .
.
![]() and
and
![]() to the renormalized variables
to the renormalized variables
![]() by
by ![]() is independent of
is independent of
![]() is that the power spectrum of the renormalized waves possesses
the precise Rayleigh-Jeans distribution, i.e.,
is that the power spectrum of the renormalized waves possesses
the precise Rayleigh-Jeans distribution, i.e., ![]() .
One of the well-known examples of such a system is the
.
One of the well-known examples of such a system is the ![]() -FPU
chain, where only the forth order nonlinear term in
-FPU
chain, where only the forth order nonlinear term in ![]() is present.
In the remainder of the article, we will focus on the
is present.
In the remainder of the article, we will focus on the ![]() -FPU to
illustrate the framework of the renormalized waves
-FPU to
illustrate the framework of the renormalized waves
![]() .
.