


Next: Dispersion relation and resonances
Up: Interactions of renormalized waves
Previous: Renormalized waves
Numerical study of the  -FPU chain
-FPU chain
Since its introduction in the early 1950s, the
study of the FPU lattice [13] has led to many great
discoveries in mathematics and physics, such as soliton
theory [3]. Being non-integrable, the FPU system also became
intertwined with the celebrated Kolmogorov-Arnold-Moser
theorem [11]. Here, we extend our results of the thermalized
 -FPU chain, which were briefly reported in [12].
-FPU chain, which were briefly reported in [12].
The Hamiltonian of the  -FPU chain is of the form
-FPU chain is of the form
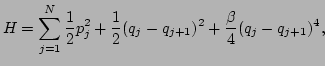 |
|
|
(29) |
where  is a parameter that characterizes the strength of
nonlinearity.
is a parameter that characterizes the strength of
nonlinearity.
The canonical equations of motion of the  -FPU chain are
-FPU chain are
To
investigate the dynamical manifestation of the renormalized
dispersion
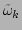 of
of
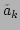 , we numerically integrate
Eq. (30). Since we study the thermal equilibrium
state [14,15,16,17] of the
, we numerically integrate
Eq. (30). Since we study the thermal equilibrium
state [14,15,16,17] of the  -FPU
chain, we use random initial conditions, i.e.,
-FPU
chain, we use random initial conditions, i.e., 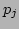 and
and 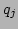 are
selected at random from the uniform distribution in the intervals
are
selected at random from the uniform distribution in the intervals
 and
and
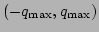 ,
respectively, with the two constraints that (i) the total momentum
of the system is zero and (ii) the total energy of the system
,
respectively, with the two constraints that (i) the total momentum
of the system is zero and (ii) the total energy of the system 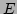 is
set to be a specified constant. We have verified that the results
discussed in the paper do not depend on details of the initial data.
Note that the behavior of
is
set to be a specified constant. We have verified that the results
discussed in the paper do not depend on details of the initial data.
Note that the behavior of  -FPU for fixed
-FPU for fixed 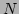 is fully
characterized by only one parameter
is fully
characterized by only one parameter 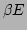 [18]. We use
the sixth order symplectic Yoshida algorithm [19] with the
time step
[18]. We use
the sixth order symplectic Yoshida algorithm [19] with the
time step 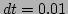 , which ensures the conservation of the total
system energy up to the ninth significant digit for a runtime
, which ensures the conservation of the total
system energy up to the ninth significant digit for a runtime
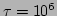 time units. In order to confirm that the system has
reached the thermal equilibrium state [20], the value of
the energy localization [21] was monitored via
time units. In order to confirm that the system has
reached the thermal equilibrium state [20], the value of
the energy localization [21] was monitored via
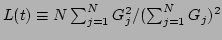 , where
, where
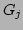 is the energy of the
is the energy of the 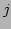 -th particle defined as
-th particle defined as
If
the energy of the system is concentrated around one site, then
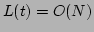 . Whereas, if the energy is uniformly distributed along
the chain, then
. Whereas, if the energy is uniformly distributed along
the chain, then 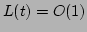 . In our simulations, in thermal
equilibrium states,
. In our simulations, in thermal
equilibrium states, 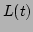 is fluctuating in the range of
is fluctuating in the range of 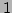 -
-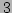 .
Since our simulation is of microcanonical ensemble, we have
monitored various statistics of the system to verify that the
thermal equilibrium state that is consistent with the Gibbs
distribution (canonical ensemble) has been reached. Moreover, we
verified that, for
.
Since our simulation is of microcanonical ensemble, we have
monitored various statistics of the system to verify that the
thermal equilibrium state that is consistent with the Gibbs
distribution (canonical ensemble) has been reached. Moreover, we
verified that, for 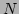 as small as 32 and up to as large as 1024,
the equilibrium distribution in the thermalized state in our
microcanonical ensemble simulation is consistent with the Gibbs
measure. We compared the renormalization factor (25) by
computing the values of
as small as 32 and up to as large as 1024,
the equilibrium distribution in the thermalized state in our
microcanonical ensemble simulation is consistent with the Gibbs
measure. We compared the renormalization factor (25) by
computing the values of
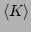 and
and
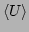 numerically and
theoretically using the Gibbs measure and found the discrepancy of
numerically and
theoretically using the Gibbs measure and found the discrepancy of
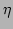 to be within
to be within 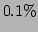 for
for 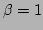 and the energy density
and the energy density
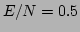 for
for  from 32 to 1024.
from 32 to 1024.
We now address numerically how the renormalized linear dispersion
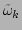 manifests itself in the dynamics of the
manifests itself in the dynamics of the  -FPU system.
We compute the spatiotemporal spectrum
-FPU system.
We compute the spatiotemporal spectrum
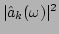 , where
, where
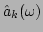 is the Fourier transform of
is the Fourier transform of
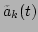 . (Note that, for
simplicity of notation, we drop a tilde in
. (Note that, for
simplicity of notation, we drop a tilde in 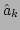 .)
.)
Figure:
The spatiotemporal spectrum
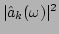 in thermal
equilibrium. The chain was modeled for
in thermal
equilibrium. The chain was modeled for 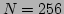 ,
, 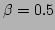 , and
, and
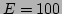 . [
. [
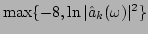 , with corresponding gray
scale, is plotted for a clear presentation]. The solid curve
corresponds to the usual linear dispersion
, with corresponding gray
scale, is plotted for a clear presentation]. The solid curve
corresponds to the usual linear dispersion
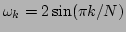 .
The dashed curve shows the locations of the actual frequency peaks
of
.
The dashed curve shows the locations of the actual frequency peaks
of
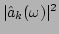 .
.
![\includegraphics[width=3in, height=2.5in]{awk_num}](img148.png) |
Figure 1 displays the spatiotemporal spectrum of
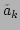 , obtained from the simulation of the
, obtained from the simulation of the  -FPU chain for
-FPU chain for
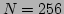 ,
, 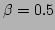 , and
, and 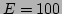 . In order to measure the value of
. In order to measure the value of
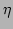 from the spatiotemporal spectrum, we use the following
procedure. For the fixed wave number
from the spatiotemporal spectrum, we use the following
procedure. For the fixed wave number  , the corresponding
renormalization factor
, the corresponding
renormalization factor 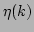 is determined by the location of
the center of the frequency spectrum
is determined by the location of
the center of the frequency spectrum
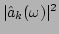 , i.e.,
, i.e.,
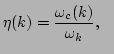 with with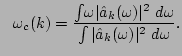 |
|
|
|
The
renormalization factor 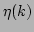 of each wave mode
of each wave mode  is shown in
Fig. 2 (inset). The numerical approximation
is shown in
Fig. 2 (inset). The numerical approximation
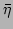 to the value of
to the value of 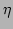 is obtained by averaging all
is obtained by averaging all 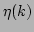 , i.e.,
, i.e.,
The renormalization factor for the case shown in
Fig. 1 is measured to be
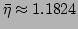 .
It can be clearly seen in Fig. 2 (inset) that
.
It can be clearly seen in Fig. 2 (inset) that 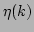 is nearly independent of
is nearly independent of  and its variations around
and its variations around
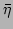 are less than
are less than 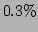 . We also compare the renormalization factor
. We also compare the renormalization factor
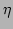 obtained from Eq. (25) (solid line in
Fig. 2 (inset)) with its numerically computed
approximation
obtained from Eq. (25) (solid line in
Fig. 2 (inset)) with its numerically computed
approximation
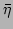 (dashed line in
Fig. 2 (inset)). Equation (25) gives the value
(dashed line in
Fig. 2 (inset)). Equation (25) gives the value
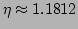 and the difference between
and the difference between 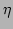 and
and
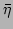 is less then
is less then 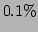 , which can be attributed to the
statistical errors in the numerical measurement.
, which can be attributed to the
statistical errors in the numerical measurement.
Figure 2:
The renormalization factor as a function of the
nonlinearity strength  . The analytical prediction
[Eq. (25)] is depicted with a solid line and the numerical
measurement is shown with circles. The chain was modeled for
. The analytical prediction
[Eq. (25)] is depicted with a solid line and the numerical
measurement is shown with circles. The chain was modeled for
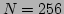 , and
, and 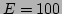 . Inset: Independence of
. Inset: Independence of  of the
renormalization factor
of the
renormalization factor 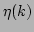 . The circles correspond to
. The circles correspond to
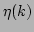 obtained from the spatiotemporal spectrum shown in
Fig. 1 [only even values of
obtained from the spatiotemporal spectrum shown in
Fig. 1 [only even values of  are shown for
clarity of presentation]. The dashed line corresponds to the mean
value
are shown for
clarity of presentation]. The dashed line corresponds to the mean
value
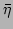 . For
. For 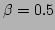 , the mean value of the
renormalization factor is found to be
, the mean value of the
renormalization factor is found to be
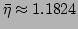 . The
variations of
. The
variations of 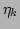 around
around
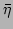 are less then
are less then 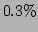 .
[Note the scale of the ordinate.] The solid line corresponds to the
renormalization factor
.
[Note the scale of the ordinate.] The solid line corresponds to the
renormalization factor 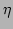 obtained from Eq. (25). For the
given parameters
obtained from Eq. (25). For the
given parameters
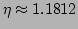 .
.
![\includegraphics[width=3in, height=2.5in]{etak_in}](img154.png) |
In Fig. 2, we plot the value of 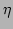 as a function of
as a function of
 for the system with
for the system with 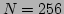 particles and the total energy
particles and the total energy
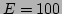 . The solid curve was obtained using Eq. (25) while
the circles correspond to the value of
. The solid curve was obtained using Eq. (25) while
the circles correspond to the value of 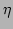 determined via the
numerical spectrum
determined via the
numerical spectrum
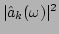 as discussed above. It can be
observed that there is excellent agreement between the theoretic
prediction and numerically measured values for a wide range of the
nonlinearity strength
as discussed above. It can be
observed that there is excellent agreement between the theoretic
prediction and numerically measured values for a wide range of the
nonlinearity strength  .
.
In the following Sections, we will discuss how the renormalization
of the linear dispersion of the  -FPU chain in thermal
equilibrium can be explained from the wave resonance point of view.
In order to give a wave description of the
-FPU chain in thermal
equilibrium can be explained from the wave resonance point of view.
In order to give a wave description of the  -FPU chain, we
rewrite the Hamiltonian (29) in terms of the renormalized
variables
-FPU chain, we
rewrite the Hamiltonian (29) in terms of the renormalized
variables
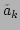 [Eq. (19)] with
[Eq. (19)] with
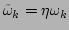 ,
,
where c.c. stands for complex conjugate, and
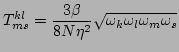 |
|
|
(33) |
is the interaction tensor coefficient. Note that, due to the
discrete nature of the system of finite size, the wave space is
periodic and, therefore, the ``momentum'' conservation is guaranteed
by the following ``periodic'' Kronecker delta functions
Here, the Kronecker 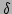 -function is equal to 1, if the sum
of all superscripts is equal to the sum of all subscripts, and 0,
otherwise.
-function is equal to 1, if the sum
of all superscripts is equal to the sum of all subscripts, and 0,
otherwise.



Next: Dispersion relation and resonances
Up: Interactions of renormalized waves
Previous: Renormalized waves
Dr Yuri V Lvov
2007-04-11
![]() -FPU chain is of the form
-FPU chain is of the form ![]() -FPU chain are
-FPU chain are ![$\displaystyle \frac{1}{2}p_j^2+\frac{1}{4}\big[(q_j-q_{j+1})^2+(q_{j-1}-q_j)^2\big]$](img134.png)
![$\displaystyle \frac{\beta}{8}\big[(q_j-q_{j+1})^4+(q_{j-1}-q_j)^4\big].$](img135.png)
![]() manifests itself in the dynamics of the
manifests itself in the dynamics of the ![]() -FPU system.
We compute the spatiotemporal spectrum
-FPU system.
We compute the spatiotemporal spectrum
![]() , where
, where
![]() is the Fourier transform of
is the Fourier transform of
![]() . (Note that, for
simplicity of notation, we drop a tilde in
. (Note that, for
simplicity of notation, we drop a tilde in ![]() .)
.)
![\includegraphics[width=3in, height=2.5in]{awk_num}](img148.png)
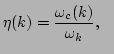 with
with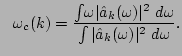
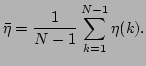
![\includegraphics[width=3in, height=2.5in]{etak_in}](img154.png)
![]() -FPU chain in thermal
equilibrium can be explained from the wave resonance point of view.
In order to give a wave description of the
-FPU chain in thermal
equilibrium can be explained from the wave resonance point of view.
In order to give a wave description of the ![]() -FPU chain, we
rewrite the Hamiltonian (29) in terms of the renormalized
variables
-FPU chain, we
rewrite the Hamiltonian (29) in terms of the renormalized
variables
![]() [Eq. (19)] with
[Eq. (19)] with
![]() ,
,