


Next: Weak turbulence theory
Up: Hamiltonian formalism for long
Previous: Rotating Nonlinear Shallow Waters
The equations for long internal waves in a rotating environment are
particularly simple when written in the isopycnal coordinates
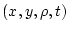 ; they take the form in (
; they take the form in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) with an
extra term
) with an
extra term
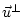 due to the Coriolis force:
due to the Coriolis force:
where
is a reference stratification profile, that we introduce here for
future convenience.
The expression for the potential vorticity in these coordinates is
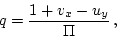 |
(25) |
and it satisfies
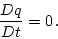 |
(26) |
Notice that the advection of potential vorticity in (![[*]](file:/usr/share/latex2html/icons/crossref.png) )
takes place exclusively along isopycnal surfaces. Therefore, an
initial distribution of potential vorticity which is constant on
isopycnals, though varying across them, will never change. Hence we
shall propose that
)
takes place exclusively along isopycnal surfaces. Therefore, an
initial distribution of potential vorticity which is constant on
isopycnals, though varying across them, will never change. Hence we
shall propose that
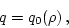 |
(27) |
where 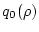 is an arbitrary function; i.e., one may assign any
constant potential vorticity to each isopycnal surface. This is a
highly nontrivial extension of the irrotational waves of the previous
sections. Extending our description further to include general
distributions of potential vorticity, varying even within surfaces of
constant density, would necessarily complicate its Hamiltonian
formulation, making it lose its natural simplicity. In fact, the
problem of interaction between vorticity and waves is that of fully
developed turbulence, which escapes the scope of our description.
However, the ``pancake-like'' distributions of potential vorticity
that we propose are common in stratified fluids, particularly the
ocean and the atmosphere. They arise due to the sharp contrast between
the magnitudes of the turbulent diffusion along and across
isopycnals. Thus potential vorticity is much more rapidly homogenized
along isopycnals than vertically, yielding the ``pancakes''.
As we show below, even waves super-imposed on such a general and
realistic distribution of potential vorticity admit a rather simple
Hamiltonian description.
is an arbitrary function; i.e., one may assign any
constant potential vorticity to each isopycnal surface. This is a
highly nontrivial extension of the irrotational waves of the previous
sections. Extending our description further to include general
distributions of potential vorticity, varying even within surfaces of
constant density, would necessarily complicate its Hamiltonian
formulation, making it lose its natural simplicity. In fact, the
problem of interaction between vorticity and waves is that of fully
developed turbulence, which escapes the scope of our description.
However, the ``pancake-like'' distributions of potential vorticity
that we propose are common in stratified fluids, particularly the
ocean and the atmosphere. They arise due to the sharp contrast between
the magnitudes of the turbulent diffusion along and across
isopycnals. Thus potential vorticity is much more rapidly homogenized
along isopycnals than vertically, yielding the ``pancakes''.
As we show below, even waves super-imposed on such a general and
realistic distribution of potential vorticity admit a rather simple
Hamiltonian description.
In order to isolate the wave dynamics satisfying the constraint
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ), we decompose the flow into a potential and a
divergence-free part as in (
), we decompose the flow into a potential and a
divergence-free part as in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ). In terms of the potentials
). In terms of the potentials
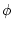 and
and 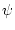 , (
, (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) and (
) and (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) yield
) yield
and, repeating the same steps as in nonlinear rotating shallow waters,
the equations in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) reduce to the pair
) reduce to the pair
This pair is Hamiltonian, with conjugated variables 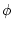 and
and  ,
i.e. it can be written as
,
i.e. it can be written as
where the Hamiltonian is given by
![\begin{displaymath}
{\cal H}= \int \left[ \frac{1}{2} \Pi \,
\left\vert\nabla...
...rho_1} \, d\rho_1\right\vert^2
\right] d\rho d\vec{r} \, .
\end{displaymath}](img124.png) |
(28) |
Again, this Hamiltonian represents the sum of the kinetic and
potential energy of the flow.
Notice the similarity of our description of internal waves with the
Hamiltonian formulation for free-surface waves introduced by Zakharov
in [31] and later by Miles in [32]. There,
it was shown that the free-surface displacement and the
three-dimensional velocity potential evaluated at the free surface
are canonical conjugate variables. In our case, the canonical
conjugate variables are also a displacement and a velocity potential,
though the velocity potential in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) is for the
two-dimensional flow along isopycnal surfaces, and the displacement
is the relative distance between neighboring isopycnal surfaces, as
described above.
) is for the
two-dimensional flow along isopycnal surfaces, and the displacement
is the relative distance between neighboring isopycnal surfaces, as
described above.
Looking back, we could have included some vorticity from early on;
there was no need to take it equal to zero, as the last section shows.
For shallow waters, it could have been any constant; for internal waves,
any function of the density. It is clear though that, if one wanted to
include arbitrary vorticity distributions, one would need to go fully
Lagrangian, to exploit the fact that vorticity is preserved along
particle paths. This would make the Hamiltonian structure less
appealingly simple.
The key steps taken here for finding a simple Hamiltonian structure
for internal waves, could be summarized as follows:
- To consider long waves in hydrostatic balance. This, together
with the choice of isopycnal coordinates, leads to a system of
equations formally equivalent to an infinite collection of
coupled shallow-water systems. This analogy allows us to
generalize the relatively simple Hamiltonian structure of
irrotational shallow-waters to the richer domain of internal
waves.
- To decouple waves from vorticity, by assuming the latter to be
either zero, constant or uniform along isopycnal surfaces,
with an arbitrary dependence on depth. This is facilitated by
the choice of a flow description in isopycnal coordinates.
- To realize that the potential
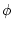 is a good candidate
canonical variable, and that its conjugate is the height
is a good candidate
canonical variable, and that its conjugate is the height 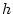 for shallow waters, and the surrogate
for shallow waters, and the surrogate  for density in the
isopycnal formulation of internal waves.
for density in the
isopycnal formulation of internal waves.
- To introduce nonlocal operators into the Hamiltonian. These
arise naturally from the ``elliptic'' constraints of
hydrostatic balance and layered potential vorticity. Despite
its unusual look, the Hamiltonian is invariably just the sum
of the standard kinetic and potential energies, integrated
over the domain.
The assumptions of hydrostatic balance and horizontally uniform
background vorticity and shear, which simplify notoriously the
description of the flows, are quite realistic for a wide range of
ocean waves.



Next: Weak turbulence theory
Up: Hamiltonian formalism for long
Previous: Rotating Nonlinear Shallow Waters
Dr Yuri V Lvov
2007-01-17
![]() ; they take the form in (
; they take the form in (![]() ) with an
extra term
) with an
extra term
![]() due to the Coriolis force:
due to the Coriolis force:
![]() ), we decompose the flow into a potential and a
divergence-free part as in (
), we decompose the flow into a potential and a
divergence-free part as in (![]() ). In terms of the potentials
). In terms of the potentials
![]() and
and ![]() , (
, (![]() ) and (
) and (![]() ) yield
) yield
![]() ) is for the
two-dimensional flow along isopycnal surfaces, and the displacement
is the relative distance between neighboring isopycnal surfaces, as
described above.
) is for the
two-dimensional flow along isopycnal surfaces, and the displacement
is the relative distance between neighboring isopycnal surfaces, as
described above.