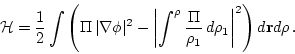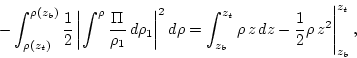Next: Linear Shallow Waters in
Up: Hamiltonian formalism for long
Previous: Nonlinear, Non-Rotating Shallow Waters
The non-dimensional equations of motion for long internal waves in an
incompressible, stratified fluid with hydrostatic balance, are given
by
where 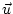 and
and  are the horizontal and vertical components of
the velocity respectively,
are the horizontal and vertical components of
the velocity respectively, 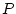 is the pressure,
is the pressure,  the density,
the density,
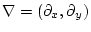 the horizontal gradient operator,
and
the horizontal gradient operator,
and
is the Lagrangian derivative following a particle.
Changing to isopycnal coordinates ( ) , where the roles of
the vertical coordinate
) , where the roles of
the vertical coordinate 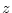 and the density
and the density  as independent and
dependent variables are reversed, the equations become:
as independent and
dependent variables are reversed, the equations become:
Here
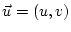 is the horizontal component of the velocity
field,
is the horizontal component of the velocity
field,
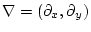 is the gradient operator
along isopycnals,
is the gradient operator
along isopycnals,
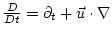 , and
, and 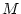 is the Montgomery potential [30],
is the Montgomery potential [30],
For flows which are irrotational along isopycnal
surfaces, we introduce the velocity potential
Such a
substitution allows us to integrate (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) once
and eliminate
) once
and eliminate 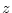 , after which these equations reduce to the pair
, after which these equations reduce to the pair
where we have introduced the variable
This variable  has at least two physical interpretations. One is
that of density in isopycnal coordinates, since
has at least two physical interpretations. One is
that of density in isopycnal coordinates, since
The other is that of a measure of the stratification, namely the
relative distance between neighboring isopycnal surfaces, since this
distance  is given by
is given by
Notice the similarity between (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) and the equations
(
) and the equations
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ) for nonlinear shallow waters. Internal
wave equations could be viewed as a system of infinitely many, coupled
shallow water equations. This analogy allows us to identify a natural
Hamiltonian structure for internal waves.
) for nonlinear shallow waters. Internal
wave equations could be viewed as a system of infinitely many, coupled
shallow water equations. This analogy allows us to identify a natural
Hamiltonian structure for internal waves.
The variable  is also the canonical conjugate of
is also the canonical conjugate of 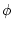 ,
,
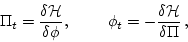 |
(9) |
under the Hamiltonian flow given by
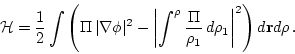 |
(10) |
The first term in this Hamiltonian clearly corresponds to the kinetic
energy of the flow; that the second term is in fact the potential
energy follows from the simple calculation
so
where 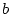 and
and 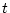 stand for bottom and top respectively, and the
boundary conditions are usually such that the integrated term at the
end is a constant.
stand for bottom and top respectively, and the
boundary conditions are usually such that the integrated term at the
end is a constant.



Next: Linear Shallow Waters in
Up: Hamiltonian formalism for long
Previous: Nonlinear, Non-Rotating Shallow Waters
Dr Yuri V Lvov
2007-01-17
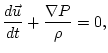
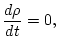
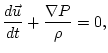
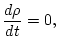
![]() ) , where the roles of
the vertical coordinate
) , where the roles of
the vertical coordinate ![]() and the density
and the density ![]() as independent and
dependent variables are reversed, the equations become:
as independent and
dependent variables are reversed, the equations become:
![]() has at least two physical interpretations. One is
that of density in isopycnal coordinates, since
has at least two physical interpretations. One is
that of density in isopycnal coordinates, since
![]() ) and the equations
(
) and the equations
(![]() ) for nonlinear shallow waters. Internal
wave equations could be viewed as a system of infinitely many, coupled
shallow water equations. This analogy allows us to identify a natural
Hamiltonian structure for internal waves.
) for nonlinear shallow waters. Internal
wave equations could be viewed as a system of infinitely many, coupled
shallow water equations. This analogy allows us to identify a natural
Hamiltonian structure for internal waves.
![]() is also the canonical conjugate of
is also the canonical conjugate of ![]() ,
,