


Next: Rotating Nonlinear Shallow Waters
Up: Hamiltonian formalism for long
Previous: Nonlinear, Non-Rotating, Internal Waves
In a rotating environment, the linearized shallow-water equations are
Here
is the velocity field, and
The Coriolis parameter 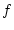 has been absorbed in the
nondimensionalization of time, so it is effectively equal to one.
has been absorbed in the
nondimensionalization of time, so it is effectively equal to one.
These equations do not preserve vorticity, so irrotationality
cannot be assumed. However, they preserve the potential
vorticity
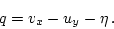 |
(11) |
The assumption corresponding to irrotationality in the non-rotating
case is therefore that of zero potential vorticity, i.e. 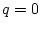 . We
can in fact generalize this hypothesis, and consider an arbitrary,
though constant, potential vorticity. We shall employ such
generalization when we consider internal waves in a rotating
environment. In order to exploit the irrotationality assumption, it is convenient to
decompose the flow into a potential and a divergence-free part:
. We
can in fact generalize this hypothesis, and consider an arbitrary,
though constant, potential vorticity. We shall employ such
generalization when we consider internal waves in a rotating
environment. In order to exploit the irrotationality assumption, it is convenient to
decompose the flow into a potential and a divergence-free part:
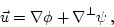 |
(12) |
where
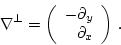 |
(13) |
In terms of 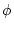 and
and 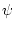 , the equations take the form
, the equations take the form
The condition of zero potential vorticity reads
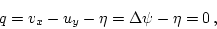 |
(15) |
so the system above reduces to
This system is Hamiltonian, with canonical variables 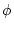 and
and
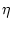 , and Hamiltonian
, and Hamiltonian
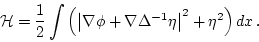 |
(18) |
Again, the Hamiltonian agrees with the total energy of the system.



Next: Rotating Nonlinear Shallow Waters
Up: Hamiltonian formalism for long
Previous: Nonlinear, Non-Rotating, Internal Waves
Dr Yuri V Lvov
2007-01-17