


Next: Nonlinear Internal Waves in
Up: Hamiltonian formalism for long
Previous: Linear Shallow Waters in
The fully nonlinear equations for shallow waters in a rotating
environment are
The statement of conservation of potential vorticity now takes the
form (Sec 12-2 in [30])
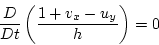 |
(21) |
(That is: the total vorticity of a vertical column of water divided by
its height remains constant as the column moves.) The unperturbed
state has
where 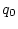 is an arbitrary
potential vorticity, so this is the hypothesis to make
for the analogue of irrotational flows:
is an arbitrary
potential vorticity, so this is the hypothesis to make
for the analogue of irrotational flows:
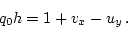 |
(22) |
We introduce the potentials 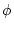 and
and 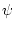 as in (
as in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ),
and use the fact that
),
and use the fact that
to rewrite (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) as
) as
Taking the divergence and the two-dimensional curl
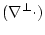 of the above
equations, we
obtain the following pair:
of the above
equations, we
obtain the following pair:
By noticing that
we can rewrite these equations, together with
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ) in the form
) in the form
The constraint (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) on the potential vorticity takes
the form
) on the potential vorticity takes
the form
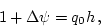 |
(23) |
under which the equations above reduce to the pair
These equations are Hamiltonian, with conjugate variables 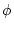 and
and 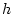 , and Hamiltonian
, and Hamiltonian
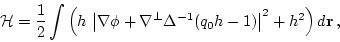 |
(24) |
representing again the sum of kinetic and potential energies.



Next: Nonlinear Internal Waves in
Up: Hamiltonian formalism for long
Previous: Linear Shallow Waters in
Dr Yuri V Lvov
2007-01-17
![$\displaystyle \phi_t + \frac{1}{2} \vert\nabla\phi+\nabla^{{\perp}}\psi\vert^2 ...
...la \cdot
\left[\Delta\psi (\nabla^{{\perp}}\phi - \nabla\psi) \right]
+ h -\psi$](img97.png)
![$\displaystyle \phi_t + \frac{1}{2} \vert\nabla\phi+\nabla^{{\perp}}\psi\vert^2 ...
...abla \cdot
\left[(1+\Delta\psi) (\nabla^{{\perp}}\phi - \nabla\psi) \right]
+ h$](img102.png)
![]() ) on the potential vorticity takes
the form
) on the potential vorticity takes
the form