Next: Appendix Up: Five-wave interaction on the Previous: 4th and 5th-order terms

Appendix

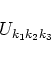
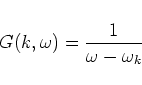
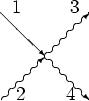
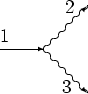
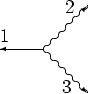
Let us introduce basic object of diagrammatic technique we use in this work.

Bare fourth order vertex with 2 incoming and 2 outgoing wave vectors:

$\begin{picture}(36,30)(0,10) \put(0,24){\vector(1,-1){12}} \multiput(11,12)(-2,-... ...){1}} \par \put(4,0){2} \put(3,24){1} \put(19,24){3} \put(18,0){4} \end{picture}$

$\begin{displaymath}W^{k_1 k_2}_{k_3 k_4}\end{displaymath}$
Bare third order vertexes U and V:

$\begin{picture}(24,30)(0,10) \put(0,12){\line(1,0){12}} \multiput(13,12)(2,2){6}... ...){\vector(1,0){1}} \par \put(0,14){1} \put(18,22){2} \put(17,0){3} \end{picture}$

$\begin{displaymath}V^{k_1}_{k_2 k_3} \end{displaymath}$

$\begin{picture}(24,30)(0,10) \put(0,12){\line(1,0){12}} \multiput(13,12)(2,2){6}... ...{\vector(-1,0){1}} \par \put(0,14){1} \put(18,22){2} \put(17,0){3} \end{picture}$

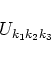
$\begin{displaymath}U_{k_1 k_2 k_3}\end{displaymath}$
Bare Green function $G(k,\omega)$ .

$\begin{picture}(24,30)(0,10) \multiput(13,12)(4,0){3}{\oval(2,1.6)[t]} \multiput... ...2,12){\vector(-1,0){12}} \put(12,16){\makebox(0,0){$k$, $\omega$}} \end{picture}$

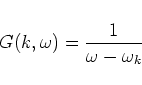
$\begin{displaymath}G(k,\omega)=\frac{1}{\omega-\omega_k}\end{displaymath}$

Note, that each vertex has just one straight line and others are wavy.

In order to calculate fourth order interaction matrix element we have to add to bare fourth order vertex all possible combinations of lower order vertexes (third order in this particular case) connected with Green function in such a way, that the resulting diagrams have 2 incoming and 2 outgoing wave vectors and having no internal loops.

It is easy to see, that the only way to fulfill these requirements is to connect 2 third order vertexes by one Green function. As the result we have 6 topologically different arrangements. The arguments and $\omega$ of internal Green function should be calculated from resonant conditions(1.1). Since we are on the resonant manifold it does not matter do we calculate arguments and $\omega$ of Green function from left or from right vertex, because it they both give the same result. This reflects the fact that two ratios in each line in square brackets of (4.3) are equal to each others. This removes extra .

$\begin{picture}(36,30)(0,10) \multiput(13,12)(4,0){2}{\oval(2,1.6)[t]} \multiput... ...4){1} \put(31,24){3} \put(30,0){4} \put(18,16){\makebox(0,0){1+2}} \end{picture}$

$\begin{displaymath} -V^{k_1+k_2}_{k_1 k_2}V^{k_3+k_4}_{k_3 k_4} \left[\frac{1}{\omega_{k_1+k_2}-\omega_{k_1}-\omega_{k_2}}\right] \end{displaymath}$

$\begin{picture}(36,30)(0,10) \multiput(13,12)(4,0){2}{\oval(2,1.6)[t]} \multiput... ...){1} \put(31,24){3} \put(30,0){4} \put(18,16){\makebox(0,0){-1-2}} \end{picture}$

$\begin{displaymath} -U_{-k_1-k_2 k_1 k_2}U_{-k_3-k_4 k_3 k_4} \left[\frac{1}{\omega_{k_1+k_2}+\omega_{k_1}+\omega_{k_2}}\right] \end{displaymath}$

$\begin{picture}(36,30)(0,10) \multiput(13,12)(4,0){2}{\oval(2,1.6)[t]} \multiput... ...4){1} \put(31,24){2} \put(30,0){4} \put(18,16){\makebox(0,0){1-3}} \end{picture}$

$\begin{displaymath} -V^{k_1}_{k_3 k_1-k_3}V^{k_4}_{k_2 k_4-k_2} \left[\frac{1}{\omega_{k_3}+\omega_{k_1-k_3}-\omega_{k_1}}\right] \end{displaymath}$

$\begin{picture}(36,30)(0,10) \multiput(13,12)(4,0){2}{\oval(2,1.6)[t]} \multiput... ...4){1} \put(31,24){2} \put(30,0){4} \put(18,16){\makebox(0,0){3-1}} \end{picture}$

$\begin{displaymath} -V^{k_2}_{k_4 k_2-k_4}V^{k_3}_{k_1 k_3-k_1} \left[\frac{1}{\omega_{k_4}+\omega_{k_2-k_4}-\omega_{k_2}}\right] \end{displaymath}$

$\begin{picture}(36,30)(0,10) \multiput(13,12)(4,0){2}{\oval(2,1.6)[t]} \multiput... ...4){1} \put(31,24){2} \put(30,0){3} \put(18,16){\makebox(0,0){1-4}} \end{picture}$

$\begin{displaymath} -V^{k_1}_{k_4 k_1-k_4}V^{k_3}_{k_2 k_3-k_2} \left[\frac{1}{\omega_{k_4}+\omega_{k_1-k_4}-\omega_{k_1}}\right] \end{displaymath}$

$\begin{picture}(36,30)(0,10) \multiput(13,12)(4,0){2}{\oval(2,1.6)[t]} \multiput... ...4){1} \put(31,24){2} \put(30,0){3} \put(18,16){\makebox(0,0){4-1}} \end{picture}$

$\begin{displaymath} -V^{k_2}_{k_3 k_2-k_3}V^{k_4}_{k_1 k_4-k_1} \left[\frac{1}{\omega_{k_3}+\omega_{k_2-k_3}-\omega_{k_2}}\right] \end{displaymath}$

Next: Appendix Up: Five-wave interaction on the Previous: 4th and 5th-order terms

Dr Yuri V Lvov 2007-01-17