- ...
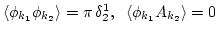
![[*]](file:/usr/share/latex2html/icons/footnote.png)
- We start by considering fields in a periodic box which is
an essential intermediate step in the definition of RPA and the new
correlators
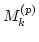 introduced later in this work. Therefore
introduced later in this work. Therefore
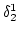 here is the Kronecker symbol. Later, we take the large
box limit corresponding to homogeneous wave turbulence.
here is the Kronecker symbol. Later, we take the large
box limit corresponding to homogeneous wave turbulence.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...'s
![[*]](file:/usr/share/latex2html/icons/footnote.png)
- This
property is typically not mentioned explicitly (but used implicitly)
when RPA is employed.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... limit.
![[*]](file:/usr/share/latex2html/icons/footnote.png)
-
Thus, assuming a finite box is an important intermediate step when
introducing the relevant to the fluctuations objects like
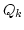 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
follows,
![[*]](file:/usr/share/latex2html/icons/footnote.png)
- We will follow the RPA approach as presented by
Galeev and Sagdeev [3] but deal with a slightly more general
case where the wave field is not restricted by the condition
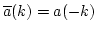 . We will also use elements of the technique
and notations of [2].
. We will also use elements of the technique
and notations of [2].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... limit
![[*]](file:/usr/share/latex2html/icons/footnote.png)
- The large box
limit implies that sums will be replaced with integrals, the Kronecker
deltas will be replaced with Dirac's deltas,
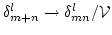 ,
where we introduced short-hand notation,
,
where we introduced short-hand notation,
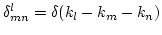 . Further we redefine
. Further we redefine
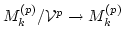 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)
![[*]](file:/usr/share/latex2html/icons/footnote.png)
- Note
that
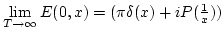 , and
, and
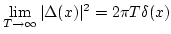 (see e.g.
[2]).
(see e.g.
[2]).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.