


Next: Time-scale separation analysis
Up: Noisy spectra, long correlations,
Previous: Noisy spectra, long correlations,
The random phase
approximation (RPA) has been popular in WT because it allows a quick
derivation of KE [1,3]. We will use RPA in this paper because
it provides a minimal model for for description of the k-space
fluctuations of the waveaction about its mean spectrum, but we will
also discuss relation to the approach of [2] which does not
assume RPA. By definition, RPA for an ensemble of complex fields
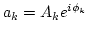 means that the phases
means that the phases 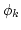 are uniformly
distributed in
are uniformly
distributed in ![$(0,2\pi]$](img5.png) and are statistically independent of each
other and of the amplitude
and are statistically independent of each
other and of the amplitude 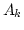 ,
,
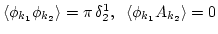
![[*]](file:/usr/share/latex2html/icons/footnote.png) . Thus, the
averaging over the phase and over the amplitude statistics can be
performed independently. In RPA, the fluctuations of the amplitudes
. Thus, the
averaging over the phase and over the amplitude statistics can be
performed independently. In RPA, the fluctuations of the amplitudes
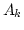 must also be decorrelated at different
must also be decorrelated at different 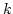 's
's![[*]](file:/usr/share/latex2html/icons/footnote.png) ,
,
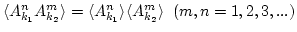 .
.
To illustrate the relation between the random phases and Gaussianity,
let us consider the fourth-order moment for which RPA gives
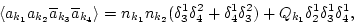 |
(1) |
where
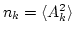 is the waveaction spectrum and
is the waveaction spectrum and
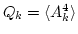 is a cumulants coefficient. The
last term in this expression appears because the phases drop out for
is a cumulants coefficient. The
last term in this expression appears because the phases drop out for
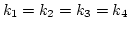 and their statistics poses no restriction on the
value of this correlator at this point. This cumulant part of the
correlator can be arbitrary for a general random-phased field whereas
for Gaussian fields
and their statistics poses no restriction on the
value of this correlator at this point. This cumulant part of the
correlator can be arbitrary for a general random-phased field whereas
for Gaussian fields 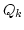 must be zero. Such a difference between the
Gaussian and the random-phased fields occurs only at a vanishingly
small set of modes with
must be zero. Such a difference between the
Gaussian and the random-phased fields occurs only at a vanishingly
small set of modes with
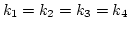 and it has been typically
ignored before because its contribution to KE is negligible.
Therefore, if the mean waveaction spectrum was the only thing we were
interested in, we could safely ignore contributions from all
(one-point) moments
and it has been typically
ignored before because its contribution to KE is negligible.
Therefore, if the mean waveaction spectrum was the only thing we were
interested in, we could safely ignore contributions from all
(one-point) moments
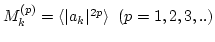 .
.
However, it is precisely moments 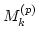 that contain information
about fluctuations of the waveaction about its mean spectrum. For
example, the standard deviation of the waveaction from its mean is
that contain information
about fluctuations of the waveaction about its mean spectrum. For
example, the standard deviation of the waveaction from its mean is
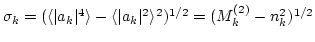 .
This quantity can be arbitrary for a general random-phased field
whereas for a Gaussian wave field the fluctuation level
.
This quantity can be arbitrary for a general random-phased field
whereas for a Gaussian wave field the fluctuation level 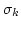 is
fixed,
is
fixed,
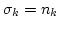 . Note that different values of moments
. Note that different values of moments
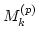 can correspond to hugely different typical wave field
realizations. In particular, if
can correspond to hugely different typical wave field
realizations. In particular, if 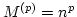 then there is no
fluctuations and
then there is no
fluctuations and 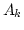 is deterministic,
is deterministic, 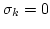 . For the
opposite extreme of large fluctuations we would have
. For the
opposite extreme of large fluctuations we would have
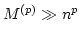 which means that the typical realization is sparse in the k-space and
is characterized by few intermittent peaks of
which means that the typical realization is sparse in the k-space and
is characterized by few intermittent peaks of 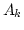 and close to zero
values in between these peaks. Note that the information about the
spectral fluctuations of the waveaction contained in the one-point
moments
and close to zero
values in between these peaks. Note that the information about the
spectral fluctuations of the waveaction contained in the one-point
moments 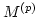 is completely erased from the multiple-point moments
by the random phases and it is precisely why these new objects play a
crucial role for the description of the fluctuations.
is completely erased from the multiple-point moments
by the random phases and it is precisely why these new objects play a
crucial role for the description of the fluctuations.
Will the waveaction fluctuations appear if they were absent initially?
Will they saturate at the Gaussian level
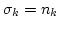 or will they
keep growing leading to the k-space intermittency? To answer these
questions, we will use RPA to derive and analyze equations for the
moments
or will they
keep growing leading to the k-space intermittency? To answer these
questions, we will use RPA to derive and analyze equations for the
moments 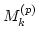 for arbitrary orders
for arbitrary orders 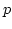 and thereby describe the
statistical evolution of the spectral fluctuations. Note that RPA,
without a stronger Gaussianity assumption, is totally sufficient for
the WT closure at any order. This allows us to study wavefields with
moments
and thereby describe the
statistical evolution of the spectral fluctuations. Note that RPA,
without a stronger Gaussianity assumption, is totally sufficient for
the WT closure at any order. This allows us to study wavefields with
moments 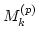 very far from their Gaussian values, which may
happen, for example, because of the choice of initial conditions or a
non-Gaussianity of the energy source in the system.
very far from their Gaussian values, which may
happen, for example, because of the choice of initial conditions or a
non-Gaussianity of the energy source in the system.
In [2] non-Gaussian fields of a rather different kind were
considered. Namely, statistically homogeneous wave fields were
considered in an infinite space which initially have decaying
correlations in the coordinate space and, therefore, smooth cumulants
in the k-space, e.g.
where 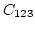 is a smooth function of
is a smooth function of 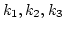 and
and
 's now mean Dirac deltas. On the other hand, by taking the
large box limit it is easy to see that our expression (1)
corresponds to a singular cumulant
's now mean Dirac deltas. On the other hand, by taking the
large box limit it is easy to see that our expression (1)
corresponds to a singular cumulant
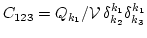 . It tends to zero when the
box volume
. It tends to zero when the
box volume 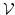 tends to infinity and yet it gives a finite
contribution to the waveaction fluctuations in this limit.
tends to infinity and yet it gives a finite
contribution to the waveaction fluctuations in this limit.![[*]](file:/usr/share/latex2html/icons/footnote.png) This singular cumulant corresponds to a small component of the
wavefield which is long-correlated - the case not covered by the
approach of [2]. On the other hand, it would be
straightforward to go beyond our RPA by adding a cumulant part of
the initial fields which tends to a smooth function of
This singular cumulant corresponds to a small component of the
wavefield which is long-correlated - the case not covered by the
approach of [2]. On the other hand, it would be
straightforward to go beyond our RPA by adding a cumulant part of
the initial fields which tends to a smooth function of 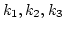 in the infinite box limit (like in [2]). However, such
cumulants would give a box-size dependent contribution to the
waveaction fluctuations which vanishes in the infinite box limit
(e.g. it would change
in the infinite box limit (like in [2]). However, such
cumulants would give a box-size dependent contribution to the
waveaction fluctuations which vanishes in the infinite box limit
(e.g. it would change 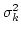 by
by
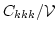 ). Thus, in
large boxes the waveaction fluctuation for the fields with smooth
cumulants is fixed at the same value as the for Gaussian fields,
). Thus, in
large boxes the waveaction fluctuation for the fields with smooth
cumulants is fixed at the same value as the for Gaussian fields,
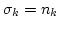 , and introduction of the singular cumulant is
essential to remove this restriction on the level of fluctuations.
On the other hand, the smooth part of the cumulants has no bearing on
the closure, as shown in [2] and on the large-box
fluctuation and, therefore, will be omitted here for
brevity and clarity of the analysis.
, and introduction of the singular cumulant is
essential to remove this restriction on the level of fluctuations.
On the other hand, the smooth part of the cumulants has no bearing on
the closure, as shown in [2] and on the large-box
fluctuation and, therefore, will be omitted here for
brevity and clarity of the analysis.



Next: Time-scale separation analysis
Up: Noisy spectra, long correlations,
Previous: Noisy spectra, long correlations,
Dr Yuri V Lvov
2007-04-11
![]() that contain information
about fluctuations of the waveaction about its mean spectrum. For
example, the standard deviation of the waveaction from its mean is
that contain information
about fluctuations of the waveaction about its mean spectrum. For
example, the standard deviation of the waveaction from its mean is
![]() .
This quantity can be arbitrary for a general random-phased field
whereas for a Gaussian wave field the fluctuation level
.
This quantity can be arbitrary for a general random-phased field
whereas for a Gaussian wave field the fluctuation level ![]() is
fixed,
is
fixed,
![]() . Note that different values of moments
. Note that different values of moments
![]() can correspond to hugely different typical wave field
realizations. In particular, if
can correspond to hugely different typical wave field
realizations. In particular, if ![]() then there is no
fluctuations and
then there is no
fluctuations and ![]() is deterministic,
is deterministic, ![]() . For the
opposite extreme of large fluctuations we would have
. For the
opposite extreme of large fluctuations we would have
![]() which means that the typical realization is sparse in the k-space and
is characterized by few intermittent peaks of
which means that the typical realization is sparse in the k-space and
is characterized by few intermittent peaks of ![]() and close to zero
values in between these peaks. Note that the information about the
spectral fluctuations of the waveaction contained in the one-point
moments
and close to zero
values in between these peaks. Note that the information about the
spectral fluctuations of the waveaction contained in the one-point
moments ![]() is completely erased from the multiple-point moments
by the random phases and it is precisely why these new objects play a
crucial role for the description of the fluctuations.
is completely erased from the multiple-point moments
by the random phases and it is precisely why these new objects play a
crucial role for the description of the fluctuations.
![]() or will they
keep growing leading to the k-space intermittency? To answer these
questions, we will use RPA to derive and analyze equations for the
moments
or will they
keep growing leading to the k-space intermittency? To answer these
questions, we will use RPA to derive and analyze equations for the
moments ![]() for arbitrary orders
for arbitrary orders ![]() and thereby describe the
statistical evolution of the spectral fluctuations. Note that RPA,
without a stronger Gaussianity assumption, is totally sufficient for
the WT closure at any order. This allows us to study wavefields with
moments
and thereby describe the
statistical evolution of the spectral fluctuations. Note that RPA,
without a stronger Gaussianity assumption, is totally sufficient for
the WT closure at any order. This allows us to study wavefields with
moments ![]() very far from their Gaussian values, which may
happen, for example, because of the choice of initial conditions or a
non-Gaussianity of the energy source in the system.
very far from their Gaussian values, which may
happen, for example, because of the choice of initial conditions or a
non-Gaussianity of the energy source in the system.