


Next: Relations between Wave Amplitudes
Up: Hamiltonian Description of Acoustic
Previous: Hamiltonian of Acoustic Turbulence
The Hamiltonian equations of motion (2.12) for the complex
canonical variables 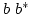 have standard form[1]
have standard form[1]
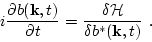 |
(43) |
For the acoustic Hamiltonian (2.17-2.19), this equation takes
the form
It is sometimes convenient to concentrate attention on steady state
turbulence, which is convenient to describe in the
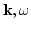 -representation. After performing a time
Fourier transform, one has instead
of (2.23),
-representation. After performing a time
Fourier transform, one has instead
of (2.23),
Hereafter we will refer to this as the basic equation of motion
for the acoustic turbulence normal variables 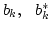 and use it
for
a statistical description of acoustic turbulence.
and use it
for
a statistical description of acoustic turbulence.



Next: Relations between Wave Amplitudes
Up: Hamiltonian Description of Acoustic
Previous: Hamiltonian of Acoustic Turbulence
Dr Yuri V Lvov
2007-01-17