Next: Bibliography
Up: Statistical Description of Acoustic
Previous: Calculation of -details
Let us write down analytical expression which correspond to one of the
diagrams (b) in Fig.1(b)
where
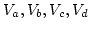 are vertices,
are vertices,
We just followed the rules of
DT and integrated over all delta-functions. From now, the analyses
will be parallel to that of appendix B. Let us use (4.16) for
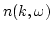 and (4.11) for
and (4.11) for 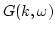 . Now we can easily
perform integration over
. Now we can easily
perform integration over 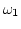 and
and 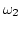 . Now, as it was
done in appendix B, introduce
. Now, as it was
done in appendix B, introduce
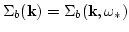 . Since all interacting wavevectors are almost parallel,
we introduce two-dimensional vectors
. Since all interacting wavevectors are almost parallel,
we introduce two-dimensional vectors 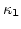 and
and 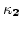 such that
such that
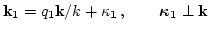 |
|
|
(133) |
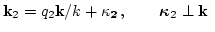 |
|
|
(134) |
We use
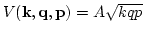 . Since
. Since
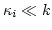 , we can expand resonance denominators in (C1)
with respect to
, we can expand resonance denominators in (C1)
with respect to 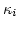 . The integrals will be dominated by
regions, where
. The integrals will be dominated by
regions, where 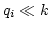 . By putting everything together, one gets
. By putting everything together, one gets
Substituting
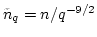 we see, that indeed, the dominant part comes from the region of small
we see, that indeed, the dominant part comes from the region of small
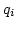 . We can estimate all these integrals to get
. We can estimate all these integrals to get
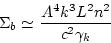 |
(137) |
where we used the small 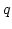 cutoff
cutoff 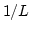 . Finally
. Finally
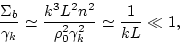 |
(138) |
and we conclude, that contribution from diagrams of type (b) on
Fig.1(b) is much less, than contribution from one-loop diagrams. But
this is not the end of the story. Let us try to estimate
contributions from diagrams of type (e) on Fig.1(b). Following the
same guidelines, we obtain
Let us again introduce 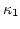 and
and 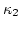 as above, and
substituting
as above, and
substituting
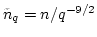 we obtain the following
estimation:
we obtain the following
estimation:
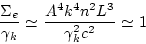 |
(139) |
Therefore we conclude, that contribution from two loop diagrams is
dominated by planar diagrams and of the order of one loop diagrams
contribution.



Next: Bibliography
Up: Statistical Description of Acoustic
Previous: Calculation of -details
Dr Yuri V Lvov
2007-01-17
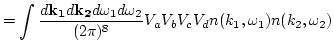
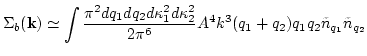
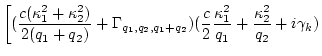
![$\displaystyle \left.
(\frac{c \kappa_2^2}{2 q_2}+ i \gamma_k)\right]^{-1}$](img551.png)