


Next: Asymptotic expansion of the
Up: Evolution of the multi-mode
Previous: Evolution of the multi-mode
Introduction of generating functionals often simplifies statistical
derivations but it can be defined differently to suit a particular
technique. For our problem, the most useful form of the generating
functional is
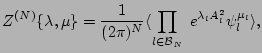 |
|
|
(10) |
where
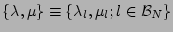 is a set of parameters,
is a set of parameters,
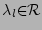 and
and
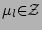 .
.
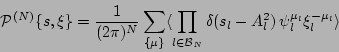 |
(11) |
where
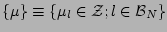 . This expression can be verified by considering mean of a
function
. This expression can be verified by considering mean of a
function
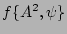 using the averaging rule (1)
and expanding
using the averaging rule (1)
and expanding  in the angular harmonics
in the angular harmonics
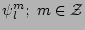 (basis functions on the unit circle),
(basis functions on the unit circle),
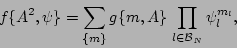 |
(12) |
where
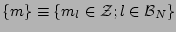 are
indices enumerating the angular harmonics. Substituting this into
(1) with PDF given by (12) and taking into
account that any nonzero power of
are
indices enumerating the angular harmonics. Substituting this into
(1) with PDF given by (12) and taking into
account that any nonzero power of 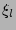 will give zero after the
integration over the unit circle, one can see that LHS=RHS, i.e.
that (12) is correct. Now we can easily represent
(12) in terms of the generating functional,
will give zero after the
integration over the unit circle, one can see that LHS=RHS, i.e.
that (12) is correct. Now we can easily represent
(12) in terms of the generating functional,
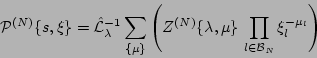 |
(13) |
where
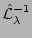 stands for inverse the Laplace transform
with respect to all
stands for inverse the Laplace transform
with respect to all 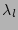 parameters and
parameters and
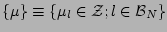 are the angular harmonics
indices.
are the angular harmonics
indices.
By definition, in RPA fields all variables  and
and 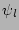 are
statistically independent and
are
statistically independent and 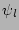 's are uniformly distributed on
the unit circle. Such fields imply the following form of the
generating functional
's are uniformly distributed on
the unit circle. Such fields imply the following form of the
generating functional
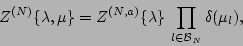 |
(14) |
where
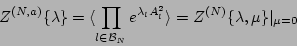 |
(15) |
is an  -mode
generating function for the amplitude statistics.
Here, the Kronecker symbol
-mode
generating function for the amplitude statistics.
Here, the Kronecker symbol 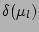 ensures
independence of the PDF from the phase factors
ensures
independence of the PDF from the phase factors 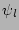 .
As a first step in validating the RPA property we will have to prove
that the generating functional
remains of form (15) up to
.
As a first step in validating the RPA property we will have to prove
that the generating functional
remains of form (15) up to 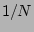 and
and
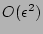 corrections over the nonlinear time
provided it has this form at
corrections over the nonlinear time
provided it has this form at 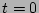 .
.



Next: Asymptotic expansion of the
Up: Evolution of the multi-mode
Previous: Evolution of the multi-mode
Dr Yuri V Lvov
2007-01-17
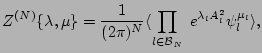
![]() and
and ![]() are
statistically independent and
are
statistically independent and ![]() 's are uniformly distributed on
the unit circle. Such fields imply the following form of the
generating functional
's are uniformly distributed on
the unit circle. Such fields imply the following form of the
generating functional