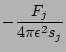 do not separate in the above equation
for the PDF. Substituting
do not separate in the above equation
for the PDF. Substituting
Obviously, the variables 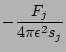 do not separate in the above equation
for the PDF. Substituting
do not separate in the above equation
for the PDF. Substituting
To answer to this question let us differentiate the discrete version
of the equation (15) with respect to ![]() 's to get
equations for the amplitude moments. We can easily see that
's to get
equations for the amplitude moments. We can easily see that
| (19) |
Similarly, one can show that the modes will remain independent over
the nonlinear time in any subset of ![]() modes with accuracy
modes with accuracy ![]() (and
(and ![]() ) if they were initially independent in every subset of
size
) if they were initially independent in every subset of
size ![]() . Namely
. Namely
| (20) |
The mismatch ![]() arises from some terms in the ZS equation with
coinciding indices
arises from some terms in the ZS equation with
coinciding indices ![]() . For
. For ![]() there is only one such term in the
there is only one such term in the
![]() -sum and, therefore, the corresponding error is
-sum and, therefore, the corresponding error is ![]() which is
much less than
which is
much less than ![]() (due to the order of the limits in
(due to the order of the limits in ![]() and
and ![]() ). However, the number of such terms grows as
). However, the number of such terms grows as ![]() and
the error accumulates to
and
the error accumulates to ![]() which can greatly exceed
which can greatly exceed
![]() for sufficiently large
for sufficiently large ![]() .
.
We see that the accuracy with which the modes remain independent in a
subset is worse for larger subsets and that the independence property
is completely lost for subsets approaching in size the entire set, ![]() . One should not worry too much about this loss because
. One should not worry too much about this loss because ![]() is
the biggest parameter in the problem (size of the box) and the modes
will be independent in all
is
the biggest parameter in the problem (size of the box) and the modes
will be independent in all ![]() -subsets no matter how large. Thus, the
statistical objects involving any finite number of particles are
factorisable as products of the one-particle objects and, therefore,
the WT theory reduces to considering the one-particle objects. This
results explains why we re-defined RPA in its relaxed ``essential
RPA'' form. Indeed, in this form RPA is sufficient for the WT closure
and, on the other hand, it remains valid over the nonlinear time. In
particular, only property (19) is needed, as far as the
amplitude statistics is concerned, for deriving the 3-wave kinetic
equation, and this fact validates this equation and all of its
solutions, including the KZ spectrum which plays an important role in
WT.
-subsets no matter how large. Thus, the
statistical objects involving any finite number of particles are
factorisable as products of the one-particle objects and, therefore,
the WT theory reduces to considering the one-particle objects. This
results explains why we re-defined RPA in its relaxed ``essential
RPA'' form. Indeed, in this form RPA is sufficient for the WT closure
and, on the other hand, it remains valid over the nonlinear time. In
particular, only property (19) is needed, as far as the
amplitude statistics is concerned, for deriving the 3-wave kinetic
equation, and this fact validates this equation and all of its
solutions, including the KZ spectrum which plays an important role in
WT.
The situation where modes can be considered as independent when taken
in relatively small sets but should be treated as dependent in the
context of much larger sets is not so unusual in physics. Consider for
example a distribution of electrons and ions in plasma. The full
![]() -particle distribution function in this case satisfies the Louville
equation which is, in general, not a separable equation. In other
words, the
-particle distribution function in this case satisfies the Louville
equation which is, in general, not a separable equation. In other
words, the ![]() -particle distribution function cannot be written as a
product of
-particle distribution function cannot be written as a
product of ![]() one-particle distribution functions. However, an
one-particle distribution functions. However, an
![]() -particle distribution can indeed be represented as a product of
-particle distribution can indeed be represented as a product of
![]() one-particle distributions if
one-particle distributions if ![]() where
where ![]() is the
number of particles in the Debye sphere. We see an interesting
transition from a an individual to collective behavior when the
number of particles approaches
is the
number of particles in the Debye sphere. We see an interesting
transition from a an individual to collective behavior when the
number of particles approaches ![]() . In the special case of the
one-particle function we have here the famous mean-field Vlasov
equation which is valid up to
. In the special case of the
one-particle function we have here the famous mean-field Vlasov
equation which is valid up to ![]() corrections (representing
particle collisions).
corrections (representing
particle collisions).