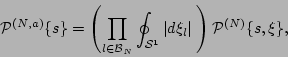Next: Weak-nonlinearity expansion.
Up: Statistical setup.
Previous: Statistical setup.
Definition of an essentially RPA field
A pure RPA fields can be defined as one in which all the
phases and amplitudes of the Fourier modes make a set of 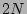 statistically independent variables and in which all phase factors
statistically independent variables and in which all phase factors
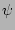 are uniformly distributed on their respective unit circles. In
such pure form RPA never survives except for in the un-interesting state
of complete thermodynamic equilibrium. However, WT closure only
requires an approximate RPA which holds up to certain order in
small
are uniformly distributed on their respective unit circles. In
such pure form RPA never survives except for in the un-interesting state
of complete thermodynamic equilibrium. However, WT closure only
requires an approximate RPA which holds up to certain order in
small 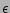 and
and 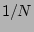 and only in a coarse-grained sense, i.e.
for the reduced
and only in a coarse-grained sense, i.e.
for the reduced 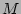 -particle objects with
-particle objects with 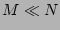 . Below we give a
relaxed definition of an (essentially) RPA property which, on one
hand, is sufficient for the WT closure and, on the other hand, is
preserved over the nonlinear time.
. Below we give a
relaxed definition of an (essentially) RPA property which, on one
hand, is sufficient for the WT closure and, on the other hand, is
preserved over the nonlinear time.
Definition: We will say that the field 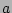 is of an
essentially RPA type if:
is of an
essentially RPA type if:
- The phase factors are statistically independent and uniformly
distributed variables up to
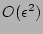 corrections, i.e.
corrections, i.e.
![\begin{displaymath}
{\cal P}^{(N)} \{s, \xi \} = {1 \over (2 \pi)^{N} } {\cal P}^{(N,a)} \{s \}
\; [1 +O({\epsilon}^2)],
\end{displaymath}](img58.png) |
(6) |
where
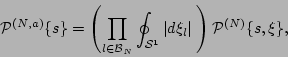 |
(7) |
is the 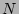 -particle amplitude PDF. In terms of the generating
functional
-particle amplitude PDF. In terms of the generating
functional
![\begin{displaymath}Z^{(N)} \{\lambda, \mu \} = Z^{(N,a)} \{\lambda \}
\, \prod_{l \in {\cal B}_N } \delta(\mu_l) \; [1 +O({\epsilon}^2)],
\end{displaymath}](img60.png) |
(8) |
where
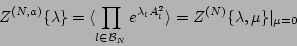 |
(9) |
is an 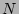 -particle generating function for the amplitude statistics.
-particle generating function for the amplitude statistics.
- The amplitude variables are independent in a coarse-grained
sense, i.e. for each
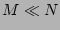 modes the
modes the 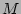 -particle amplitude PDF is
equal to the product of the one-particle PDF's up to
-particle amplitude PDF is
equal to the product of the one-particle PDF's up to 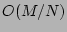 and
and
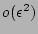 corrections,
corrections,
![\begin{displaymath}
{\cal P}^{(M,a)}_{j_1, j_2, \dots , j_M} =
P^{(a)}_{j_1}...
..._2} \dots P^{(a)}_{j_M} \; [1 +
O(M/N) + O({\epsilon}^2)].
\end{displaymath}](img64.png) |
(10) |
As a first step in validating the RPA property we will have to prove
that the generating functional remains of the form (8) over the
nonlinear time provided it has this form at 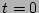 .
.



Next: Weak-nonlinearity expansion.
Up: Statistical setup.
Previous: Statistical setup.
Dr Yuri V Lvov
2007-01-17
![]() statistically independent variables and in which all phase factors
statistically independent variables and in which all phase factors
![]() are uniformly distributed on their respective unit circles. In
such pure form RPA never survives except for in the un-interesting state
of complete thermodynamic equilibrium. However, WT closure only
requires an approximate RPA which holds up to certain order in
small
are uniformly distributed on their respective unit circles. In
such pure form RPA never survives except for in the un-interesting state
of complete thermodynamic equilibrium. However, WT closure only
requires an approximate RPA which holds up to certain order in
small ![]() and
and ![]() and only in a coarse-grained sense, i.e.
for the reduced
and only in a coarse-grained sense, i.e.
for the reduced ![]() -particle objects with
-particle objects with ![]() . Below we give a
relaxed definition of an (essentially) RPA property which, on one
hand, is sufficient for the WT closure and, on the other hand, is
preserved over the nonlinear time.
. Below we give a
relaxed definition of an (essentially) RPA property which, on one
hand, is sufficient for the WT closure and, on the other hand, is
preserved over the nonlinear time.
![]() is of an
essentially RPA type if:
is of an
essentially RPA type if: