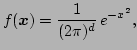Next: Linear theory without a
Up: text
Previous: Introduction
Linear dynamics of the GP equation
We will now develop a WKB theory for small-scale wave-packets,
described by a linearized GP equation, with and without the presence
of a background condensate. As is traditional with any WKB-type method
we assume the existence of a scale separation
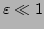 , as
explained in section
, as
explained in section ![[*]](file:/usr/share/latex2html/icons/crossref.png) . In this analysis we will take
. In this analysis we will take 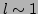 so that any spatial derivatives of a given large-scale quantity
(e.g. the potential
so that any spatial derivatives of a given large-scale quantity
(e.g. the potential 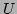 or the condensate) are of order
or the condensate) are of order
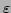 . The transition to WKB phase-space is achieved through
the application of the Gabor transform [23],
. The transition to WKB phase-space is achieved through
the application of the Gabor transform [23],
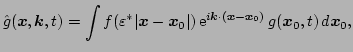 |
(2) |
where 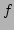 is an arbitrary function fastly decaying at infinity.
For our purposes it will be sufficient to consider a Gaussian of the form
where
is an arbitrary function fastly decaying at infinity.
For our purposes it will be sufficient to consider a Gaussian of the form
where 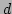 is the number of space dimensions. The parameter
is the number of space dimensions. The parameter
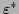 is small and such that
is small and such that
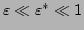 . Hence, our kernel
. Hence, our kernel 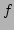 varies at the
intermediate-scale. A Gabor transform can therefore be thought of as a
localized Fourier transform, and in the limit
varies at the
intermediate-scale. A Gabor transform can therefore be thought of as a
localized Fourier transform, and in the limit
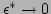 becomes an exact Fourier transform. Physically, one can view a Gabor
transform as a wavepacket distribution function over positions
becomes an exact Fourier transform. Physically, one can view a Gabor
transform as a wavepacket distribution function over positions
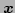 and wavevectors
and wavevectors 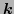 .
.
Subsections



Next: Linear theory without a
Up: text
Previous: Introduction
Dr Yuri V Lvov
2007-01-23
![]() , as
explained in section
, as
explained in section ![]() . In this analysis we will take
. In this analysis we will take ![]() so that any spatial derivatives of a given large-scale quantity
(e.g. the potential
so that any spatial derivatives of a given large-scale quantity
(e.g. the potential ![]() or the condensate) are of order
or the condensate) are of order
![]() . The transition to WKB phase-space is achieved through
the application of the Gabor transform [23],
. The transition to WKB phase-space is achieved through
the application of the Gabor transform [23],