


Next: Wavepacket dynamics on a
Up: Linear dynamics of the
Previous: Linear dynamics of the
Linearizing the GP equation, to investigate the behavior of
wavepackets 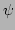 without the presence of a condensate, we obtain the
usual linear Schrödinger equation:
without the presence of a condensate, we obtain the
usual linear Schrödinger equation:
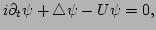 |
(3) |
where 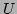 is a slowly varying potential. Let us apply the Gabor
transformation to (
is a slowly varying potential. Let us apply the Gabor
transformation to (![[*]](file:/usr/share/latex2html/icons/crossref.png) ). Note that the Gabor transformation
commutes with the Laplacian, so that
). Note that the Gabor transformation
commutes with the Laplacian, so that
 . Also note that
where we have neglected the quadratic and higher order terms in
. Also note that
where we have neglected the quadratic and higher order terms in
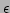 because
because 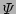 changes on a much shorter scale than the
large scale function
changes on a much shorter scale than the
large scale function 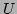 . Combining the Gabor transformed equation
with its complex conjugate we find the following WKB transport
equation,
. Combining the Gabor transformed equation
with its complex conjugate we find the following WKB transport
equation,
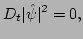 |
(4) |
where
represents the total time derivative along the wavepacket trajectories
in phase-space. The ray equations are used to describe wavepacket
trajectories in
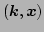 phase-space,
phase-space,
The frequency 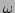 , in this case, is given by
, in this case, is given by
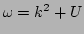 ,
(again we use the notation
,
(again we use the notation
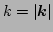 ). Equations (
). Equations (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) and
(
) and
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ) are nothing more than the famous Ehrenfest theorem
from quantum mechanics. According to (
) are nothing more than the famous Ehrenfest theorem
from quantum mechanics. According to (![[*]](file:/usr/share/latex2html/icons/crossref.png) ), the wavepackets
will get reflected by the potential at points
), the wavepackets
will get reflected by the potential at points 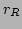 where
where
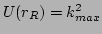 . We will now move on to consider linear wavepackets in
the presence of a background condensate.
. We will now move on to consider linear wavepackets in
the presence of a background condensate.



Next: Wavepacket dynamics on a
Up: Linear dynamics of the
Previous: Linear dynamics of the
Dr Yuri V Lvov
2007-01-23