Introduction

Bose-Einstein condensate (BEC) was first observed in 1995 in atomic vapors of $^{87}$Rb [1], $^7$Li [2] and $^{23}$Na [3]. Typically, the gas of atoms is confined by a magnetic trap [1], and cooled by laser and evaporative means. Although the basic theory for the condensation was known from the classical works of Bose [4] and Einstein [5], the experiments on BEC stimulated new theoretical work in the field (an excellent review of this material is given in [6]).

A lot of theoretical results about condensate dynamics are based on the assumption that the condensate band can be characterized by some temperature $T$ and chemical potential $\mu$, the quantities which are clearly defined only for gases in thermodynamic equilibrium. Often, however, the condensation is so rapid that the gas is in a very nonequilibrium state and hence, one requires the use of a kinetic rather than a thermodynamic theory [9,10,11]. An approach using the quantum kinetic equation was developed by Gardiner et al [9,10] who used some phenomenological assumptions about the scattering amplitudes. Phenomenology is unavoidable in the general case due to an extreme dynamical complexity of quantum gases the atoms in which interact among themselves and exhibit wave-particle dualism. Most phenomenological assumptions are intuitive or arise from a physical analogy and are hard to validate (or to prove wrong) theoretically. In particular, it was proposed that the ground BEC states act onto the higher levels via an effective potential. In the present paper we are going to examine this assumption in a special case of large occupation numbers, i.e. when the system is more like a collection of interacting waves rather than particles and which allows a systematic theoretical treatment. In what follows we show systematically that such an assumption is not true for such systems. For dilute gases, with a large number of atoms at low temperatures, one obtains the Gross-Pitaevskii (GP) equation for the condensate order parameter [7,8]:

$$i \partial_{t}\psi +\triangle \psi - \vert\psi\vert^{2}\psi -U\psi= 0,$$ (1)

where the potential $U$ is a given function of coordinate, see for example figure . We emphasize that the area of validity of GP equation is restricted to a narrow class of the low-temperature BEC growth experiments and the latest stages in other BEC experiments. However, we will study the GP equation because it provides an important limiting case for which one can rigorously test the phenomenological assumptions made for more general systems. We would like to abandon the approach where the system is artificially divided into a $T=0$ condensate state and a thermal ``cloud'' because this ``cloud'' in reality is far from the thermodynamic equilibrium and we believe that this fact affects the BEC dynaimcs in an essential way. As in many other non-equilibrium and turbulent systems, fluxes of the conserved quantities through the phase space are more relevant for the theory here than the temperature and the chemical potential. Performance of a thermodynamic theory here would be as poor as a description of waterfalls by a theory developed for lakes. Again, the GP equation is used in our work for both the ground and the excited states which limits our analysis only to the low temperature and high occupation number situations.

In fact the idea of using GP equation for describing BEC kinetics is not new and it goes back to work of Kagan et al [11], who used a kinetic equation for waves systematically derived from the GP equation ignoring the trapping potential and assuming turbulence to be spatially homogeneous [12]. A similar method has been used to investigate optical turbulence [13]. Classical weak turbulence theory yields a closed kinetic equation for the long time behavior of the energy spectrum without having to make unjustifiable assumptions about the statistics of the processes [14,15,16,18,22,24]. Second, the kinetic equation admits classes of exact equilibrium solutions [14,19,20]. These can be identified as pure Kolmogorov spectra [12,13,14], namely equilibria for which there is a constant spectral flux of one of the invariants, the energy,

$$E = \int [\vert\nabla \psi\vert^2 + \frac{1}{2} \vert\psi\vert^4] \, d {\bf x},$$

and the ``number of particles'',

$$N =\int \vert\psi\vert^2 \, d {\bf x}.$$

A very important property of the particle cascade is that it transfers the particles to the small $k$ values (inverse cascade). This transfer will lead to an accumulation at small $k$'s which is precisely the mechanism of the BE condensation, see figure 1. The energy cascade is toward high values of $k$ which eventually will lead to ``spilling'' over the potential barrier corresponding to an evaporative cooling, see figure 1. After the formation of strong condensate one can no longer use weak turbulence theory, as the weak turbulence theory assumes small amplitudes. However, one can reformulate the theory using a linearization around the condensate, (as oppose to linearization around the 0 state), as in [13]. Consequently this changes the dominant system interactions from 4-wave to 3-wave processes.

Figure: Turbulent cascades of energy $E$ and particle number $N$.

[width=.6]fig1.eps

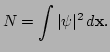
Kolmogorov-type energy distributions over the levels (scales) are dramatically different from any thermodynamic equilibrium distributions. Thus, the condensation and the cooling rates will also be significantly different from those obtained from theories based on the assumptions of a thermodynamic equilibrium and the existence of a Boltzmann distribution. As an example, a finite-time condensation was predicted by Kagan, Svistunov and Shlyapnikov [11], whose work was based on the theory of weak homogeneous turbulence.

However, application of the theory of homogeneous turbulence to the GP equation has its limitations. Indeed, when the external potential is not ignored in the GP equation, the turbulence is trapped and is, therefore, intrinsically inhomogeneous (e.g. a turbulent spot). Additional inhomogeneity of the turbulence arises because of the condensate, which in the GP equation case is itself coordinate dependent. This means, in particular, that the theory of homogeneous turbulence cannot describe the ground state effect onto the confining properties of the gas and thereby test the effective potential approach. The present paper is aimed at removing this pitfall via deriving an inhomogeneous weak turbulence theory.

The effects of the coordinate dependent potential and condensate can most easily be understood using a wavepacket (WKB) formalism that is applicable if the wavepacket wavelength $l$ is much shorter than the characteristic width of the potential well $L$,

$$\varepsilon = \frac{l}{L} \ll 1.$$

The coordinate dependent potential and the condensate distort the wavepackets so that their wavenumbers change. This has a dramatic effect on nonlinear resonant wave interactions because now waves can only be in resonance for a finite time. The goal of our paper is to use the ideas developed for the GP equation without the trapping potential and to combine them with the WKB formalism in order to derive a weak turbulence theory for a large set of random waves described by the GP equation.

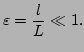Note that idea to combine the kinetic equation with WKB to describe weakly nonlinear dynamics of wave (or quantum) excitations is quite old and can be traced back to Khalatnikov's theory of Bose gas (1952) and Landau's theory of the Fermi fluids (1956), see e.g. in [27]. It has also been widely used to describe kinetics of waves in plasmas, e.g. [28,29,30,31]. For plasmas, such a formalism was usually derived from the first principles. However, only phenomenological models based on an experimentally measured dispersion curves have been proposed so far for the superfluid kinetics. In this paper, we offer for the first time a consistent derivation starting from the GP equation which allows us to correct the existing BEC phenomenology at least for the special cases when the GP equation is applicable.

Technically, the most nontrivial new element of our theory appears through the linear dynamics (WKB) whereas modifications of the nonlinear part (the collision integral) are fairly straightforward. Thus, we start with a detailed consideration of the linear dynamics in section . Previously, linear excitations to the ground state were considered by Fetter [17] who used a test function approach to derive an approximate dispersion relation for these excitations. Fetter pointed out an uncertainty of the boundary conditions to be used at the ground state reflection surface. The WKB theory for BEC which is for the first time developed in the present paper allows an asymptotically rigorous approach which, among other things, allows to clarify the role of the ground state reflection surface. Indeed, as we will see in section 3, the WKB theory is essentially different in the case when the condensate ground state is weak and can be neglected from the case of strongly nonlinear ground state. No suitable WKB description exists for the intermediate case in which the linear and the nonlinear effects are of the same order. However, in the Thomas-Fermi regime the layer of the intermediate condensate amplitudes is extremely narrow due to the exponential decay of the amplitude beyond the ground state reflection surface. This allowed us to combine the two WKB descriptions into one by formally re-writing the equations in such a way that they are correct in the limits of both weak and strong condensate. These equations will be wrong in the thin layer of intermediate condensate amplitudes, but this will not have any effect on the overall dynamics of wavepackets because they pass this layer too quickly to be affected by it.

In section 4 for the first time we present a Hamiltonian formulation of the WKB equations and derive a cannonical Hamiltonian the form of which is general for all WKB systems and not only BEC. The Hamiltonian formulation is needed to prepare the scene for the weak turbulence theory. In section 5 we apply weak turbulence theory to write a closed kinetic equation for wave action. This kinetic equation has a coordinate dependence of the frequency delta functions. Notice that coordinate dependence of the wave frequency has a profound effect on the nonlinear dynamics. The resonant wave interactions can now take place only over a limited range of wave trajectories which makes such interactions similar to the collision of discrete particles.