


Next: Summary
Up: text
Previous: Weakly nonlinear GP equation
Now, by analogy with homogeneous weak turbulence, we define the
waveaction spectrum as
where averaging is performed over the random initial phases. Note
that this definition is slightly different to the usual definition of
the turbulence spectrum in homogeneous turbulence, i.e. the definition
constructed from Fourier transforms,
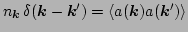 . Indeed, a Gabor transform can be
viewed as a finite-box Fourier transform, where
. Indeed, a Gabor transform can be
viewed as a finite-box Fourier transform, where
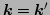 in the
definition of the spectrum and one replaces
in the
definition of the spectrum and one replaces
 with
the box volume
with
the box volume  .
.
Multiplying (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) by
) by
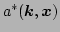 and combining the
resulting equation with its complex conjugate, we get a generalization
of (
and combining the
resulting equation with its complex conjugate, we get a generalization
of (![[*]](file:/usr/share/latex2html/icons/crossref.png) ):
):
with
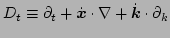 . Note, that in the case of homogeneous
turbulence, using the random phase assumption, in the above equation,
would lead to the RHS becoming zero. This means that the nontrivial
kinetic equation appears only in higher orders of the nonlinearity.
For the inhomogeneous case, the nontrivial effect of the nonlinearity
appears even at this (second) order. This can be seen via a frequency
correction which, in turn, modifies the wave trajectories. This
effect was considered by Zakharov et al [31] and it is
especially important in systems where such frequency corrections
result in modulational instabilities followed by collapsing events. In
our case the nonlinearity is ``defocusing'' and, therefore, such an
effect is less important. Indeed, in what follows we will neglect this
effect as, at sufficiently small ratios of the inhomogeneity and
turbulence intensity parameters,
. Note, that in the case of homogeneous
turbulence, using the random phase assumption, in the above equation,
would lead to the RHS becoming zero. This means that the nontrivial
kinetic equation appears only in higher orders of the nonlinearity.
For the inhomogeneous case, the nontrivial effect of the nonlinearity
appears even at this (second) order. This can be seen via a frequency
correction which, in turn, modifies the wave trajectories. This
effect was considered by Zakharov et al [31] and it is
especially important in systems where such frequency corrections
result in modulational instabilities followed by collapsing events. In
our case the nonlinearity is ``defocusing'' and, therefore, such an
effect is less important. Indeed, in what follows we will neglect this
effect as, at sufficiently small ratios of the inhomogeneity and
turbulence intensity parameters,
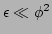 , wave collision
events are a far more dominant process.
, wave collision
events are a far more dominant process.
Let us introduce notations
and
Then, we have the following equation for the 4th-order moment,
where we denote
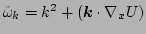 . Note
that the first two terms on the RHS of this equation can be obtained
one from another by exchanging
. Note
that the first two terms on the RHS of this equation can be obtained
one from another by exchanging 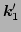 and
and 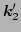 , whereas the last
two terms - by exchanging
, whereas the last
two terms - by exchanging 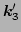 and
and 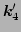 . To solve this
equation, one can use the random phase assumption which is
standard for the derivation of a weak homogeneous turbulence
theory and which allows one to express the 6th-order moment in terms
of the 2nd-order correlators. For homogeneous turbulence, the validity
of this assumption was examined by Newell et al
[18,33]
who showed that initially Gaussian turbulence
(characterized by random independent phases) remains Gaussian for the
energy cascade range whereas in the particle cascade range deviations
from Gaussianity grow toward low
. To solve this
equation, one can use the random phase assumption which is
standard for the derivation of a weak homogeneous turbulence
theory and which allows one to express the 6th-order moment in terms
of the 2nd-order correlators. For homogeneous turbulence, the validity
of this assumption was examined by Newell et al
[18,33]
who showed that initially Gaussian turbulence
(characterized by random independent phases) remains Gaussian for the
energy cascade range whereas in the particle cascade range deviations
from Gaussianity grow toward low 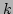 values. However, these deviations
remain small over a large range of
values. However, these deviations
remain small over a large range of 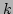 for small initial amplitudes
and the random phase assumption can be used for these scales. Note
that the deviations from Gaussianity at low
for small initial amplitudes
and the random phase assumption can be used for these scales. Note
that the deviations from Gaussianity at low 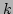 correspond to the
physical process of building a coherent condensate state. The results
of [18,33] obtained for homogeneous GP
turbulence will hold for trapped turbulence too because inhomogeneity
has a neutral effect on the phase correlations. Indeed, according to
the linear WKB equations the phases propagate unchanged along the
rays. Thus we write
correspond to the
physical process of building a coherent condensate state. The results
of [18,33] obtained for homogeneous GP
turbulence will hold for trapped turbulence too because inhomogeneity
has a neutral effect on the phase correlations. Indeed, according to
the linear WKB equations the phases propagate unchanged along the
rays. Thus we write
here we have used the shorthand notations,
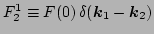 and
and
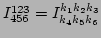 .
Using this expression in (
.
Using this expression in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) we have
) we have
Notice that the
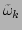 terms get replaced by
terms get replaced by 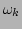 ,
since the
,
since the
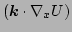 terms drop out on the resonant
manifold. Let us integrate this equation over the period
terms drop out on the resonant
manifold. Let us integrate this equation over the period 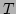 which is
less than both the slow WKB time
which is
less than both the slow WKB time
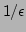 and the nonlinear time
and the nonlinear time
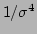 . Then, one can ignore the time dependence in
. Then, one can ignore the time dependence in 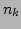 on
the RHS of the above equation and we can take
on
the RHS of the above equation and we can take
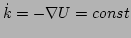 on the LHS.
on the LHS.
The resulting equation can be easily integrated along the
characteristics (rays) which in the limit
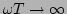 gives
gives
Note that to derive a similar expression in the theory of
homogeneous weak turbulence one usually introduces an artificial
``dissipation'' to circumvent the pole and to get the correct sign in
front of the delta function (see e.g. [14]). The roots of this
problem can be found even at the level of the linear dynamics, where
the use of Laplace (rather than Fourier) transforms provides a
mathematical justification for the introduction of such a
dissipation. However, in our case there is no need for us to introduce
such a dissipation because inhomogeneity removes the degeneracy in the
system.
Substituting (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) into
(
) into
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ) we get the main equation describing weak
turbulence, the four-wave kinetic equation
) we get the main equation describing weak
turbulence, the four-wave kinetic equation
where,
We can see that the main difference between the kinetic equation for
inhomogeneous media and homogeneous turbulence
[11,12,13,22] is that the partial time derivative on
the LHS is replaced by the full time derivative along the rays.
Further, the frequency 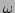 and spectrum
and spectrum 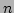 are now functions not
only of the wavenumber but also of the coordinate.
are now functions not
only of the wavenumber but also of the coordinate.
The same is true for the case when the ground state condensate is
important for the wave dynamics [13]. The main interaction
mechanism now become three wave interactions, with the kinetic
equation
where
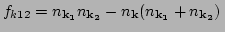 . Here,
. Here, 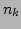 ,
,  and
and  are given by
expressions (
are given by
expressions (![[*]](file:/usr/share/latex2html/icons/crossref.png) ), (
), (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) and (
) and (![[*]](file:/usr/share/latex2html/icons/crossref.png) )
respectively and the expression for the interaction coefficient
)
respectively and the expression for the interaction coefficient
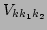 can be found in [13]. Three-wave interactions
always dominate over the four-wave process when
can be found in [13]. Three-wave interactions
always dominate over the four-wave process when
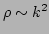 (because
(because 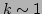 and
and 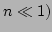 . In the case
. In the case
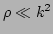 , the
relative importance of the three-wave and the four-wave processes can
be established by comparing the characteristic times associated with
these processes. The characteristic time of the three wave
interactions for
, the
relative importance of the three-wave and the four-wave processes can
be established by comparing the characteristic times associated with
these processes. The characteristic time of the three wave
interactions for
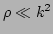 is
is
Thus, the 3-wave process will
dominate the 4-wave one if the condensate is stronger than the waves, i.e. if
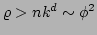 .
.



Next: Summary
Up: text
Previous: Weakly nonlinear GP equation
Dr Yuri V Lvov
2007-01-23
![]() ) by
) by
![]() and combining the
resulting equation with its complex conjugate, we get a generalization
of (
and combining the
resulting equation with its complex conjugate, we get a generalization
of (![]() ):
):
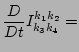
![]() gives
gives