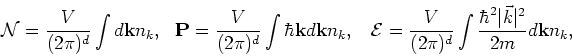 |
(3.1) |
The collision integral in (2.20) has the following constants of
motion
In this article we will be dealing with the isotropic case only, and,
for simplicity, neglect the spin degree of freedom. Therefore we
simplify the collision integral by averaging it over all
angles. First, we change variables from particles momentum ![]() to the particle kinetic energy
to the particle kinetic energy
We introduce
![]() and rewrite the kinetic equation as
and rewrite the kinetic equation as
However, the thermodynamic equilibrium is not the most general
steady (equilibrium) solution of the kinetic equation and indeed in
some cases has little relevance. The solutions we are most interested
in are those which describe the steady state reached between
ranges of frequencies where particles and energy are added to or
removed from the system. These regions, where there is no pumping or
dumping, are called "windows of transparency" or "inertial
ranges". In particular, we have in mind the following
situation. Particles and energy are added to the system in a narrow
range of intermediate frequencies about ![]() . Particles and energy
are drained from the system in a range of frequencies about
. Particles and energy
are drained from the system in a range of frequencies about
![]() and for
and for
![]() . Because of conservation of
energy and particles in the inertial ranges between
. Because of conservation of
energy and particles in the inertial ranges between ![]() and
and ![]() and between
and between ![]() and
and ![]() where there is no pumping or damping and
because the relations between particle number
where there is no pumping or damping and
because the relations between particle number ![]() and energy
density
and energy
density
![]() , we will find that a net flux of energy to the
higher frequencies must be accompanied by a net flux of particles to
lower frequencies as it might be expected by analogy with classical
wave turbulence. The presence of sources and sinks drives the system
away from the thermodynamic equilibrium. Therefore, in the windows of
transparency,
, we will find that a net flux of energy to the
higher frequencies must be accompanied by a net flux of particles to
lower frequencies as it might be expected by analogy with classical
wave turbulence. The presence of sources and sinks drives the system
away from the thermodynamic equilibrium. Therefore, in the windows of
transparency,
![]() and
and
![]() , the system can also
relax to equilibrium distributions corresponding to a finite flux of
particles and energy flowing through these windows from the sources to
the sinks. These are the new solutions of the QKE. The number of such
finite flux solutions corresponds to the number of conserved densities
(here two,
, the system can also
relax to equilibrium distributions corresponding to a finite flux of
particles and energy flowing through these windows from the sources to
the sinks. These are the new solutions of the QKE. The number of such
finite flux solutions corresponds to the number of conserved densities
(here two, ![]() and
and ![]() , or
, or ![]() and
and
![]() ) of the QKE.
) of the QKE.
To demonstrate the existence of such solutions, we rewrite the KE in
the following form:
The relevant equation kinetic equation, which includes the presence of sources and
sinks is
| (3.10) |
We are particularly interested in the solutions for which ![]() particles
per unit time and
particles
per unit time and ![]() units of energy per
unit time are fed to the system in a narrow frequency
window about
units of energy per
unit time are fed to the system in a narrow frequency
window about
![]() . We will assume that the flux of particles passing
through the left (right) window
. We will assume that the flux of particles passing
through the left (right) window
![]() (
(
![]() ) is
) is ![]() (
(![]() ) and the flux of energy though the right (left) window is
) and the flux of energy though the right (left) window is ![]() (
(![]() ). We will also assume that the sinks consume all the particles and
energy that reach them. Then (see Figure 1)
). We will also assume that the sinks consume all the particles and
energy that reach them. Then (see Figure 1)
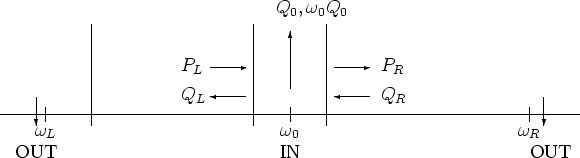
Figure 1
The first two relations in (3.14) express
conservation of particles and energy. The second two express the fact
that, in order to maintain equilibrium, the rate of particle
destruction at ![]() is the rate of energy destroyed there divided by
the energy per particle. Likewise the amount of energy destroyed at
is the rate of energy destroyed there divided by
the energy per particle. Likewise the amount of energy destroyed at
![]() (which absorption, in the context of application discussed in
the section 5, will be due to semiconductor lasing) must be
(which absorption, in the context of application discussed in
the section 5, will be due to semiconductor lasing) must be ![]() times the number of particles absorbed there. Solving (3.14)
we obtain
times the number of particles absorbed there. Solving (3.14)
we obtain
Solutions to (3.16), (3.17) have not been investigated
even in the classical case. In the classical case, Zakharov (see,
e.g., [22],[23]) had found the pure Kolmogorov solutions
![]() ,
, ![]() which turns out to have power law behavior
which turns out to have power law behavior
![]() . Likewise, in the bosonic case, several authors have
attempted to find power law solutions which essentially balance the
quadratic terms in
. Likewise, in the bosonic case, several authors have
attempted to find power law solutions which essentially balance the
quadratic terms in
![]() with a finite energy
flux. However, in the differential approximation, there are no power
law solutions.
with a finite energy
flux. However, in the differential approximation, there are no power
law solutions.
In many cases it may be that whenever
![]() ,
, ![]() may
not be all that much smaller than
may
not be all that much smaller than ![]() . In particular, in order to
exploit these solutions in the context of semiconductor lasers, it is
advantageous to have
. In particular, in order to
exploit these solutions in the context of semiconductor lasers, it is
advantageous to have ![]() close enough to
close enough to ![]() to minimize energy
losses (the ratio
to minimize energy
losses (the ratio
![]() ) but
far enough away to facilitate pumping unimpeded by
Pauli blocking. We return to this application after introducing an
enormous simplification for
) but
far enough away to facilitate pumping unimpeded by
Pauli blocking. We return to this application after introducing an
enormous simplification for ![]() which gives a very good qualitative
description of the collision integral.
which gives a very good qualitative
description of the collision integral.