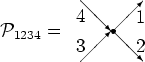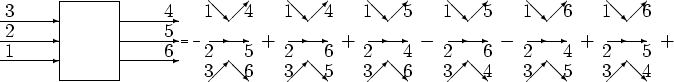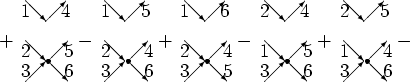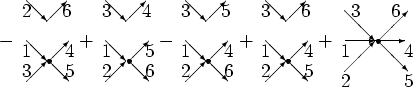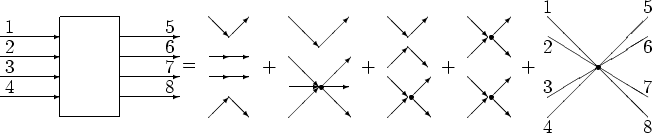Next: Bibliography
Up: text
Previous: Figure Captions
In this section we present simple diagrams
which can help one to visualize the definition of cumulants. These
diagrams are only meant as an aid to visualize the correlation
contribution and should not be confused with other diagrams such as
Feymann diagrams. The following pictures are intended to illustrate
the ways to
factorize  ,
,  and
and  . Let us denote
by square boxes operator averages according to (2.9), so that two
connected arrows present
. Let us denote
by square boxes operator averages according to (2.9), so that two
connected arrows present 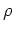 (2 operator expectation value), and
(2 operator expectation value), and
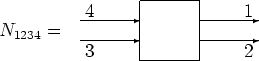
Let us present cumulants in the form of vertices, with incoming arrows
representing the arguments of annihilation operators, and the outgoing
the arguments of creation operators. Then the second order cumulant
(which is the same as the two operator average) is represented by two
arrows:
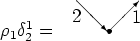
The fourth order cumulant is represented by four arrows:
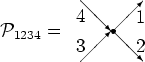
so that the definition of fourth order cumulant
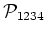 is
is
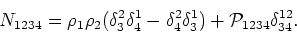 |
(9.1) |
This partition can be represented graphically as

Because of the commutation relations (2.1), if we
interchange two indices corresponding to two creation or two
annihilation operators, the average should change its sign, for
example:
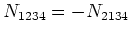 . The definitions of cumulants should not
contradict this property, so each product of lower order cumulants
should be either positive or negative, depending upon whether it
corresponds to an odd or even permutation. This explains the negative
sign in from of
. The definitions of cumulants should not
contradict this property, so each product of lower order cumulants
should be either positive or negative, depending upon whether it
corresponds to an odd or even permutation. This explains the negative
sign in from of
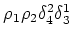 term in
(9.1). Similarly, the definition of the sixth order cumulant
term in
(9.1). Similarly, the definition of the sixth order cumulant
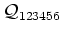 is
is
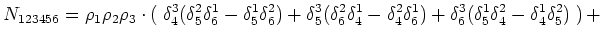 |
|
|
|
![$\displaystyle \rho _3[+{{\cal{P}}}_{1256}\delta ^{3}_{4}\delta ^{12}_{56}-{{\ca...
...\delta ^{1}_{6}\delta ^{23}_{45}]\cr+ {{{\cal Q}}}_{123456}\delta ^{123}_{456}.$](img419.png) |
|
|
(9.2) |
This partition can be represented as
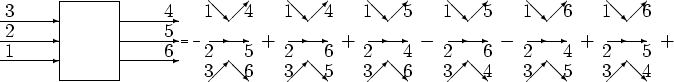
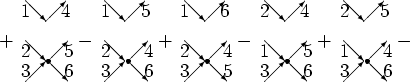
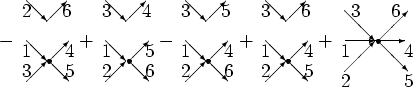
cm Again, because of the commutation relations
(2.1), if we interchange two indices corresponding to
two creation or two annihilation operators, the average should change
its sign, for example:
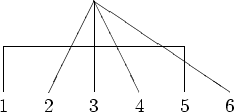
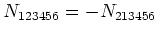 . The picture below
illustrates a simple algorithm of counting the parity of
permutation by counting the number of crossing between lines
connecting different arguments. In the example below, one sees that
the parity of
. The picture below
illustrates a simple algorithm of counting the parity of
permutation by counting the number of crossing between lines
connecting different arguments. In the example below, one sees that
the parity of
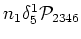 term in the expansion of
term in the expansion of 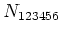 is
odd (because of the odd number of crossings), so the product is
negative.
is
odd (because of the odd number of crossings), so the product is
negative.
In the same manner, the definition of
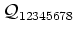
can be presented as
cm
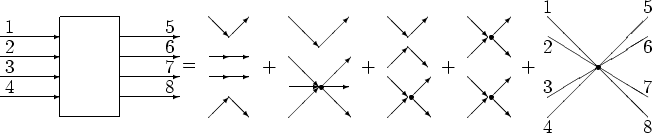
Because of the large amount of terms in this case, we show only
schematically the
factorization of
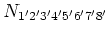 . One has to choose all
possible permutations of indices, corresponding to different
topologies putting ``annihilation'' arguments to the incoming and
``creation'' arguments to the outgoing arrows.
. One has to choose all
possible permutations of indices, corresponding to different
topologies putting ``annihilation'' arguments to the incoming and
``creation'' arguments to the outgoing arrows.



Next: Bibliography
Up: text
Previous: Figure Captions
Dr Yuri V Lvov
2007-01-31