


Next: Acknowledgments
Up: Semiconductor Lasers and Kolmogorov
Previous: Model
We show the results in figures 2, 3, and 4. First, to test accuracy,
we show, in Figure 2, the relaxation of (6) to a pure Fermi-Dirac
spectrum in the window
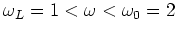 . The boundary conditions
correspond to
. The boundary conditions
correspond to 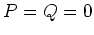 at both ends. We then modify boundary
conditions to read
at both ends. We then modify boundary
conditions to read 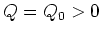 and
and 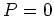 at both ends. Next, in Figure 3 and 4, we show the
results of two experiments in which we compare the efficiencies of two
experiments in which we arrange to (i) pump broadly so that the effective
carrier distribution equilibrium has zero flux and (ii) pump carriers and
energy into a narrow band of frequencies about
at both ends. Next, in Figure 3 and 4, we show the
results of two experiments in which we compare the efficiencies of two
experiments in which we arrange to (i) pump broadly so that the effective
carrier distribution equilibrium has zero flux and (ii) pump carriers and
energy into a narrow band of frequencies about  and simulate this by
specifying carrier and energy flux rates
and simulate this by
specifying carrier and energy flux rates 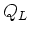 and
and
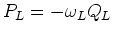 (
(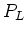 chosen so that the energy absorbed by the laser is consistent with
the number of carriers absorbed there) at the boundary
chosen so that the energy absorbed by the laser is consistent with
the number of carriers absorbed there) at the boundary
 .
.
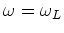 is the frequency at which the system lases.
is the frequency at which the system lases.
In both cases, the rate of addition of carriers and energy is
(approximately) the same. The results support the idea that it is
worth exploring the exploitation of the finite flux equilibrium. The
carrier density of the equilibrium solutions at  is small thus
making pumping more efficient there. The output of the laser is
greater by a factor of 10. While we do not claim that, when all
effects are taken account of, this advantage will necessary remain, we
do suggest that the strategy of using finite flux equilibrium
solutions of the Quantum Boltzmann equation is worth further
exploration.
is small thus
making pumping more efficient there. The output of the laser is
greater by a factor of 10. While we do not claim that, when all
effects are taken account of, this advantage will necessary remain, we
do suggest that the strategy of using finite flux equilibrium
solutions of the Quantum Boltzmann equation is worth further
exploration.



Next: Acknowledgments
Up: Semiconductor Lasers and Kolmogorov
Previous: Model
Dr Yuri V Lvov
2007-01-17
![]() is small thus
making pumping more efficient there. The output of the laser is
greater by a factor of 10. While we do not claim that, when all
effects are taken account of, this advantage will necessary remain, we
do suggest that the strategy of using finite flux equilibrium
solutions of the Quantum Boltzmann equation is worth further
exploration.
is small thus
making pumping more efficient there. The output of the laser is
greater by a factor of 10. While we do not claim that, when all
effects are taken account of, this advantage will necessary remain, we
do suggest that the strategy of using finite flux equilibrium
solutions of the Quantum Boltzmann equation is worth further
exploration.