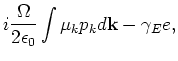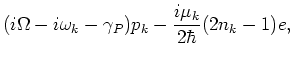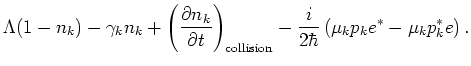Next: Results
Up: Semiconductor Lasers and Kolmogorov
Previous: Introduction
We present the results of a numerical simulation of a greatly simplified
model of semiconductor lasing in which we use parameter values which are
realistic but make fairly severe approximations in which we (a) assume
that the densities of electrons and holes are the same (even though their
masses differ considerably) (b) ignore carrier recombination losses
and (c) model the collision integral by a differential approximation
[1], [2], [3]
in
which the principal contributions to wavevector quartets satisfying
(1) are assumed to come from nearby neighbors. Despite the
brutality of the approximations, the results we obtain are qualitatively
similar to what we obtain using more sophisticated and
complicated descriptions.
The semiconductor Maxwell-Bloch equations are [4],[5],
Here  and
and 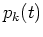 are the electric field and polarization at
momentum
are the electric field and polarization at
momentum 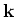 envelopes of the carrier wave
envelopes of the carrier wave
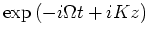 where
where 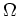 is the cavity frequency (we assume single mode operation only)
and
is the cavity frequency (we assume single mode operation only)
and 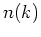 is the carrier density for electrons and holes. The constants
is the carrier density for electrons and holes. The constants
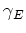 ,
, 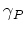 model electric field and homogeneous broadening losses,
model electric field and homogeneous broadening losses,
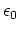 is dielectric constant,
is dielectric constant, 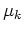 is the weighting accorded to
different
is the weighting accorded to
different 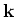 momentum (modeled by
momentum (modeled by
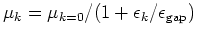 ),
), 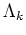 and
and 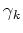 represent carrier pumping and damping. In (4), the collision term
is all important and is given by
represent carrier pumping and damping. In (4), the collision term
is all important and is given by
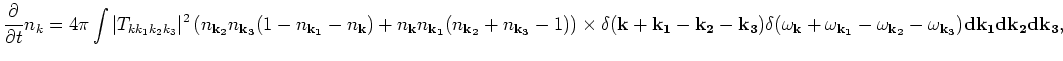 |
|
|
(5) |
where
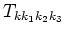 is the coupling
coefficient measuring mutual electron and hole interactions. We make the
weak assumption that all fields are isotropic and make a convenient
transformation from
is the coupling
coefficient measuring mutual electron and hole interactions. We make the
weak assumption that all fields are isotropic and make a convenient
transformation from 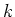 (
(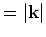 ) to
) to 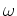 via the dispersion
relation
via the dispersion
relation
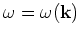 defining the carrier density
defining the carrier density 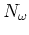 by
by
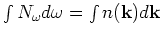 or
or
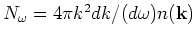 .
Then, in the differential approximation, (5) can be written as
both,
.
Then, in the differential approximation, (5) can be written as
both,
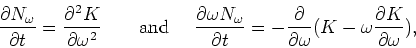 |
(6) |
with
where 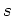 is the number computed from the dispersion relation, the
dependence of
is the number computed from the dispersion relation, the
dependence of
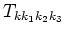 on
on 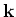 and dimensions (
and dimensions (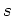 is of the order of
is of the order of
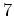 for semiconductors.) The conservation forms of the equations for
for semiconductors.) The conservation forms of the equations for
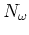 and
and
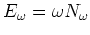 allow us identify
allow us identify
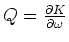 (positive if carriers flow from high to low momenta) and
(positive if carriers flow from high to low momenta) and
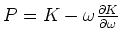 (positive if energy flows from low
to high momenta) as the fluxes of carriers and energy respectively.
Moreover, the equilibrium solutions are now all transparent. The general
stationary solution of (6) is the integral of
(positive if energy flows from low
to high momenta) as the fluxes of carriers and energy respectively.
Moreover, the equilibrium solutions are now all transparent. The general
stationary solution of (6) is the integral of 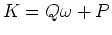 which
contains four parameters, two (chemical potential and temperature)
associated with the fact that
which
contains four parameters, two (chemical potential and temperature)
associated with the fact that 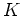 is a second derivative, and two constant
fluxes
is a second derivative, and two constant
fluxes 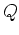 and
and 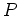 of carriers and energy. The Fermi-Dirac solution
of carriers and energy. The Fermi-Dirac solution
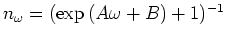 , the solution of
, the solution of 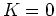 , has zero flux. We
will now solve (2), (3) and (4) after angle
averaging (4) and replacing
, has zero flux. We
will now solve (2), (3) and (4) after angle
averaging (4) and replacing
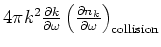 by
by
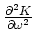 . The value of the constant
. The value of the constant 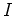 is
chosen to ensure that solutions of (6) relax in a time of 100 fs.
is
chosen to ensure that solutions of (6) relax in a time of 100 fs.



Next: Results
Up: Semiconductor Lasers and Kolmogorov
Previous: Introduction
Dr Yuri V Lvov
2007-01-17