


Next: Calculation of -details
Up: Statistical Description of Acoustic
Previous: Conclusion
Here we
state without proof the set of rules for writing down diagrammatic
series:
- In order to write down all diagrams for
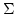 and
and 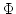 of 2n
order in vertices, one should draw 2n vertices and connect them with
each other by lines
of 2n
order in vertices, one should draw 2n vertices and connect them with
each other by lines 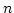 and
and 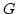 in all possible ways. Two ends must
be left free. If both ends are straight, we shall get a diagram for
in all possible ways. Two ends must
be left free. If both ends are straight, we shall get a diagram for
 ; if one of them is wavy, this will be a diagram
for
; if one of them is wavy, this will be a diagram
for
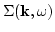 .
.
- The diagrams for
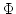 and
and 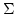 containing closed loops in GF
are absent. This follows from the fact that the Wyld's DT appears
from glued trees.
containing closed loops in GF
are absent. This follows from the fact that the Wyld's DT appears
from glued trees.
- There is no mass operator with two wavy ends in DT.
- In the diagrams for
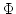 (for
(for 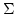 ) one can pass from every
vertex along the
) one can pass from every
vertex along the 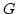 lines to the entrance and to the exit in a single
way.
lines to the entrance and to the exit in a single
way.
- In every diagram for
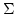 there is a single root linking
the entrance and exit along the
there is a single root linking
the entrance and exit along the 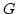 lines - the backbone of the
diagram. The rest
lines - the backbone of the
diagram. The rest 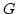 lines of the diagrams may be called the rips.
lines of the diagrams may be called the rips.
- The diagrams for
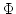 contain the basic cross section in which they
may be cut in a single way into two parts only at lines
contain the basic cross section in which they
may be cut in a single way into two parts only at lines
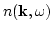 .
.
- Every
 vertex is entered by one arrow and excited by two. The
vertex is entered by one arrow and excited by two. The
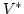 vertex is entered by two arrows and exited by one.
vertex is entered by two arrows and exited by one.
One can show (see [12]) that rules (3-7) follows from (1-2).
The rules of reading diagrams are the follows:
- Write down product of DT objects (double correlator, Green function or
vertex) (with corresponding arguments) corresponding to each element
of the diagram.
- Write down delta-functions in 4-momenta for
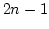 vertices in such a
way, that the sum of entering 4-momenta is equal to the sum of
exciting ones. One of vertices (for example the one corresponding to
the end of the diagram) does not contain the delta function.
vertices in such a
way, that the sum of entering 4-momenta is equal to the sum of
exciting ones. One of vertices (for example the one corresponding to
the end of the diagram) does not contain the delta function.
- Perform integration along all internal lines of diagram :
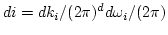 where
where 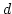 is space dimension.
is space dimension.
- Then you have to multiply diagram by
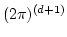 .
.
- To multiply diagram by
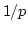 where
where 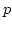 is the number of elements in
its symmetry group.
is the number of elements in
its symmetry group.
For example diagrams (a1), (a2) and (a3) correspond to the following
analytical expressions: q
We defined here the following shorthand notation,
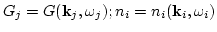 In the same way one can
find analytical expressions for
In the same way one can
find analytical expressions for
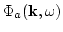 :
:
Analytical expressions for s the 4-th order diagrams (two-loop
diagrams) will be shown in Appendix C.



Next: Calculation of -details
Up: Statistical Description of Acoustic
Previous: Conclusion
Dr Yuri V Lvov
2007-01-17