In the first numerical experiment, Run I of Table 1,
we examine statistical stability of the GM spectrum of a freely decaying system,
i.e. without external forcing.
The GM spectrum with the cut-off in large isopycnal and density wavenumbers
is employed as the initial energy spectrum.
The cut-off is introduced to avoid decreasing accuracy of the pseudo-spectral method.
The initial phases of complex amplitude, ![]() , are given by uniformly distributed random numbers in
, are given by uniformly distributed random numbers in ![]() .
Figure 1 shows the initial spectrum and the energy spectrum after about 35 hours in ocean time.
If the GM spectrum were to be a universal steady state for this numerical run, it would change very little.
Instead,
the density exponents rapidly change from
.
Figure 1 shows the initial spectrum and the energy spectrum after about 35 hours in ocean time.
If the GM spectrum were to be a universal steady state for this numerical run, it would change very little.
Instead,
the density exponents rapidly change from ![]() to
to ![]() only after
only after ![]() days.
This spectral change occurs faster than dissipation affects
with timescale estimated to be about 50 days at
days.
This spectral change occurs faster than dissipation affects
with timescale estimated to be about 50 days at ![]() .
Therefore it appears that
the GM spectrum is not a stable universal spectrum in the wavenumber region
.
Therefore it appears that
the GM spectrum is not a stable universal spectrum in the wavenumber region ![]() at least for this numerical experiment.
This suggests that
the diffusion approximation of the kinetic equation (McComas, 1977; McComas & Müller, 1981),
which predicts that energy spectra are rapidly relaxed to the GM spectrum,
may not be fully appropriate.
at least for this numerical experiment.
This suggests that
the diffusion approximation of the kinetic equation (McComas, 1977; McComas & Müller, 1981),
which predicts that energy spectra are rapidly relaxed to the GM spectrum,
may not be fully appropriate.
![\includegraphics[scale=0.8]{spectra2d_psfrag.eps}](img110.png)
|
Hoping to find a statistically steady state,
we then performed a forced-damped simulation, Run II (see Table 1).
The external forcing is added to 24 small wavenumbers whose frequencies are close to ![]() such that
such that
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
The two-dimensional energy spectrum in near statistically steady state
obtained in this simulation is shown in Fig. 2.
We observe that there is a significant energy accumulation around
.
The two-dimensional energy spectrum in near statistically steady state
obtained in this simulation is shown in Fig. 2.
We observe that there is a significant energy accumulation around ![]() ,
i.e. the horizontally longest waves.
Note that linear frequency given by dispersion relation is exactly
,
i.e. the horizontally longest waves.
Note that linear frequency given by dispersion relation is exactly ![]() when
when ![]() .
Similarly, accumulation of energy around
.
Similarly, accumulation of energy around ![]() corresponds to accumulation of energy in near-inertial frequencies.
This is precisely what happens in the ocean!
Indeed all versions of the GM spectra
have an integrable singularity in near-inertial frequencies
such as
corresponds to accumulation of energy in near-inertial frequencies.
This is precisely what happens in the ocean!
Indeed all versions of the GM spectra
have an integrable singularity in near-inertial frequencies
such as
![]() (Garrett & Munk, 1972,1975,1979), indicating significant energy contents in near-inertial waves.
Such an accumulation can be explained quantitatively as a result of
a parametric subharmonic instability (Furuich, Hibiya & Niwa, 2005) which
arises in small isopycnal wavenumbers.
(Garrett & Munk, 1972,1975,1979), indicating significant energy contents in near-inertial waves.
Such an accumulation can be explained quantitatively as a result of
a parametric subharmonic instability (Furuich, Hibiya & Niwa, 2005) which
arises in small isopycnal wavenumbers.
![\includegraphics[scale=0.71]{spectra_k_psfrag.eps}](img120.png) ![\includegraphics[scale=0.71]{spectra_m_psfrag.eps}](img121.png)
|
Figure 3 shows integrated spectra,
![]() and
and
![]() ,
and cross-sectional spectra,
,
and cross-sectional spectra, ![]() and
and ![]() obtained from two-dimensional energy spectrum shown in Fig. 2.
The integrated spectra are
obtained from two-dimensional energy spectrum shown in Fig. 2.
The integrated spectra are
![]() and
and
![]() .
The exponents are not too far from the large-wavenumber self-similar form of GM spectrum,
that is
.
The exponents are not too far from the large-wavenumber self-similar form of GM spectrum,
that is
![]() .
The exponents are obtained with the least-square method
in the intervals of
.
The exponents are obtained with the least-square method
in the intervals of ![]() for
for
![]() and that of
and that of
![]() for
for
![]() .
.
![\includegraphics[scale=0.71]{exp_k_psfrag.eps}](img128.png) ![\includegraphics[scale=0.71]{exp_m_psfrag.eps}](img129.png)
|
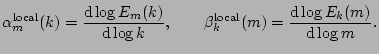 |
(22) |
![\includegraphics[scale=0.71]{spectra_k_s1_psfrag.eps}](img143.png) ![\includegraphics[scale=0.71]{spectra_m_s1_psfrag.eps}](img144.png)
|
![\includegraphics[scale=0.71]{spectra_k_s2_psfrag.eps}](img145.png) ![\includegraphics[scale=0.71]{spectra_m_s2_psfrag.eps}](img146.png)
|
![\includegraphics[scale=0.71]{exp_k_s1_psfrag.eps}](img147.png) ![\includegraphics[scale=0.71]{exp_m_s1_psfrag.eps}](img148.png)
|
![\includegraphics[scale=0.71]{exp_k_s2_psfrag.eps}](img149.png) ![\includegraphics[scale=0.71]{exp_m_s2_psfrag.eps}](img150.png)
|
Next,
we investigate the influence of this accumulation of energy on inertial wavenumbers.
To achieve this goal,
we perform two numerical runs III and IV in Table 1.
These two runs are different by value of inertial frequencies ![]() (see Table 1).
The difference of values of inertial frequencies influences the rate of formation of the accumulation around the horizontally longest waves.
After about
(see Table 1).
The difference of values of inertial frequencies influences the rate of formation of the accumulation around the horizontally longest waves.
After about ![]() days from the initial time
when all the wavenumbers have extremely small energy,
the system is still transient
and the accumulation of energy around the horizontally longest waves has not developed strongly.
The timescales of the formation of the accumulation,
which are determined by nonlinear interactions among the long waves,
are much longer than those of the inertial wavenumbers.
The energy spectrum of the case with
days from the initial time
when all the wavenumbers have extremely small energy,
the system is still transient
and the accumulation of energy around the horizontally longest waves has not developed strongly.
The timescales of the formation of the accumulation,
which are determined by nonlinear interactions among the long waves,
are much longer than those of the inertial wavenumbers.
The energy spectrum of the case with
![]() rad/sec has only weak accumulation
since all the forced wavenumbers have frequencies greater than
rad/sec has only weak accumulation
since all the forced wavenumbers have frequencies greater than ![]() ,
far from the linear frequencies of the wavenumbers that constitute the accumulation.
The energy spectrum of the case with
,
far from the linear frequencies of the wavenumbers that constitute the accumulation.
The energy spectrum of the case with ![]() rad/sec has moderate accumulation,
which is stronger than that of the case with
rad/sec has moderate accumulation,
which is stronger than that of the case with
![]() rad/sec
and is weaker than that of Run II.
rad/sec
and is weaker than that of Run II.
The integrated and cross-sectional spectra and their power-law exponents
after ![]() days are shown
in Figs. 6, 7, 8 and 9.
The least-square fitting to obtain the power-law exponents is made in the intervals of
days are shown
in Figs. 6, 7, 8 and 9.
The least-square fitting to obtain the power-law exponents is made in the intervals of
![]() .
When the accumulation of energy around the horizontally longest waves is weak enough,
the energy spectrum is close to the double-power
.
When the accumulation of energy around the horizontally longest waves is weak enough,
the energy spectrum is close to the double-power
![]() in large isopycnal and density wavenumbers.
On the other hand,
the energy spectrum does not have double-power laws
in the region when the accumulation is moderate.
It is caused by contamination of the inertial region due to the accumulation.
Another double-power law
in large isopycnal and density wavenumbers.
On the other hand,
the energy spectrum does not have double-power laws
in the region when the accumulation is moderate.
It is caused by contamination of the inertial region due to the accumulation.
Another double-power law
![]() appears
in small isopycnal and density wavenumbers.
Again, we point out that
the exponents of cross-sectional spectra are also sufficiently different from those of the integrated spectra and the GM spectrum.
Therefore, in combination with Run II,
it appears that
the accumulation of energy around the horizontally longest waves strongly affects
statistical properties in the inertial region.
appears
in small isopycnal and density wavenumbers.
Again, we point out that
the exponents of cross-sectional spectra are also sufficiently different from those of the integrated spectra and the GM spectrum.
Therefore, in combination with Run II,
it appears that
the accumulation of energy around the horizontally longest waves strongly affects
statistical properties in the inertial region.
![\includegraphics[scale=0.8]{rd1_psfrag.eps}](img157.png)
|
To further illustrate this point, and to investigate the importance of nonlocal interactions in the wavenumber space,
we perform Run V of Table 1.
There we choose the initial condition
same as the Run I but with no energy in ![]() and
and ![]() .
The energy spectrum after about
.
The energy spectrum after about ![]() days is denoted by
days is denoted by
![]() .
The energy spectrum developed from the GM spectrum in Run I that is shown in Fig. 1(right)
is denoted by
.
The energy spectrum developed from the GM spectrum in Run I that is shown in Fig. 1(right)
is denoted by
![]() .
Figure 10 shows the relative difference defined as
.
Figure 10 shows the relative difference defined as
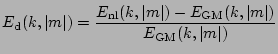 |
(23) | ||
| (24) |