Numerical simulation

Numerical simulations presented in this work were performed on a single-processor workstation (2.5GHz, 1Gb RAM). We performed a direct numerical simulation, integrating the dynamical equations of motion (4) and (5) using pseudo-spectral method with resolution of $256\times256$ wavenumbers. Numerical integrator used for advancing in time was RK7(8) presented in [31]. Time step was $\frac{T_{min}}{35}$ where $T_{min}$ is the period of the shortest wave on the axis. Approximate processor time for this work was 4.5 weeks.

In our numerical experiment, we force the system in the $k$-space ring $k_* < k < k^*$ with $k_* =6$ and $k^* = 9$. This ring is located at the low wavenumber part of the $k$-space in order to generate energy cascade toward large $k$'s, but we deliberately avoid forcing even longer waves ($k<6$) because our experience shows that this would lead to undesirable strong anisotropic effects. In the ring, we fix the shape to coincide with the ZF spectrum, $<\vert a_{\mathbf{k}}(t)\vert^{2}>\sim k^{-4}$, and hence we set $\vert\eta _{\mathbf{k} }\vert \sim k^{-7/4}$, $\vert\Psi _{\mathbf{k}}\vert \sim k^{-9/4}$. These fixed amplitudes were then multiplied by random phase factors. Thus, surface $\eta _{\mathbf{k}}$ and velocity potential $\Psi_{\mathbf{k}}$ were set to $2\pi ^{3} \, e^{i \theta _{\mathbf{k}}} \ast k^{\alpha _{\mathbf{k}}}$, where $\theta _{\mathbf{k}}$ were uniformly distributed in $[0,2\pi ]$ and

$$\alpha _{k}=x\left\{ \begin{array}{cc} \left[ 1+\left( \frac{k_{\... .../4} & \hbox{if} \;k\in \left( k^{\ast },\frac{N}{2}\right) \end{array} \right\}$$

where $x=-7/4$ for the surface and $x=-9/4$ for velocity potential. Damping was applied in both small and large wavenumber regions. At small wavenumbers inside the forcing ring, we applied an adaptive damping to prevent formation of undesirable ``condensate'' which could spoil isotropy and locality of scale interactions. At large wavenumbers, damping is needed to absorb the energy cascade and, therefore, to avoid ``bottleneck'' spectrum accumulation near the cutoff wavenumber. In our simulations, we implemented the damping as a low-pass filter $\gamma _{\mathbf{k}}$ applied to the $k$-space variables at each time step. The damping function had the form

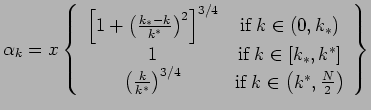$$\gamma _{\mathbf{k}}=\left\{ \begin{array}{cc} 5\left( k-6\right)... ... \left[ 6,64\right] \\ 0.028\left( k-64\right) ^{2} & k>64 \end{array} \right\}$$

Nonlinearity parameter was set to $\varepsilon =2\cdot 10^{-2}$, which is a sufficient value to produce a resonance broadening for supporting energy cascade.