Let us consider a wavefield in a periodic square basin of side ![]() and
let the Fourier representation of this field be
and
let the Fourier representation of this field be ![]() where index
where index
![]() marks the mode with wavenumber
marks the mode with wavenumber
![]() on the grid in the
on the grid in the ![]() -dimensional Fourier space.
Discrete
-dimensional Fourier space.
Discrete ![]() -space is important for formulating the statistical
problem. For simplicity let us assume that there is a cut-off
wavenumber
-space is important for formulating the statistical
problem. For simplicity let us assume that there is a cut-off
wavenumber ![]() so that thee is no modes with wavenumber
components greater than
so that thee is no modes with wavenumber
components greater than ![]() , which is always the case in
numerical simulation. In this case, the total number of modes is
, which is always the case in
numerical simulation. In this case, the total number of modes is
![]() and index
and index ![]() will only take values in a finite
box,
will only take values in a finite
box,
![]() which is centered at 0 and
all sides of which are equal to
which is centered at 0 and
all sides of which are equal to ![]() . To consider homogeneous
turbulence, the large box (i.e. continuous
. To consider homogeneous
turbulence, the large box (i.e. continuous ![]() ) limit,
) limit,
![]() , will have to be taken later.
, will have to be taken later.
Let us write the complex ![]() as
as
![]() where
where ![]() is a
real positive amplitude and
is a
real positive amplitude and ![]() is a phase factor which takes
values on
is a phase factor which takes
values on
![]() , a unit circle centered at zero in the
complex plane. The most general statistical object in WT [5]
is the
, a unit circle centered at zero in the
complex plane. The most general statistical object in WT [5]
is the ![]() -mode joint PDF
-mode joint PDF
![]() defined as the probability
for the wave intensities
defined as the probability
for the wave intensities ![]() to be in the range
to be in the range
![]() and for the phase factors
and for the phase factors ![]() to be on the unit-circle
segment between
to be on the unit-circle
segment between ![]() and
and
![]() for all
for all
![]() .
.
The fundamental statistical property of the wavefield in WT is that
all the amplitudes ![]() and phase factors
and phase factors ![]() are independent
statistical variables and that all
are independent
statistical variables and that all ![]() 's are uniformly
distributed on
's are uniformly
distributed on
![]() .
This kind of statistics was introduced in [6,4,5] and called ``Random
Phase and Amplitude'' (RPA) field.
In terms of the PDF, we say that the field
.
This kind of statistics was introduced in [6,4,5] and called ``Random
Phase and Amplitude'' (RPA) field.
In terms of the PDF, we say that the field ![]() is of
RPA type if it can be product-factorized,
is of
RPA type if it can be product-factorized,
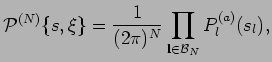 |
(14) |
Note that in this formulation
the distributions of
![]() remain unspecified and, therefore, the amplitudes do not have to be deterministic
(as in earlier works using RPA) nor do they have to correspond to Gaussianity,
remain unspecified and, therefore, the amplitudes do not have to be deterministic
(as in earlier works using RPA) nor do they have to correspond to Gaussianity,
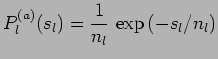 |
(15) |
Importantly, RPA formulation involves independent phase factors
![]() and not phases
and not phases ![]() . Firstly, the phases
would not be convenient because the mean value of the phases is
evolving with the rate equal to the nonlinear frequency correction
[5]. Thus one could not say that they are ``distributed
uniformly from
. Firstly, the phases
would not be convenient because the mean value of the phases is
evolving with the rate equal to the nonlinear frequency correction
[5]. Thus one could not say that they are ``distributed
uniformly from ![]() to
to ![]() ''. Moreover the mean fluctuation of the
phase distribution is also growing and they quickly spread beyond
their initial
''. Moreover the mean fluctuation of the
phase distribution is also growing and they quickly spread beyond
their initial ![]() -wide interval [5]. But perhaps even more
important, it was shown in [5] that
-wide interval [5]. But perhaps even more
important, it was shown in [5] that ![]() 's build mutual
correlations on the nonlinear timescale whereas
's build mutual
correlations on the nonlinear timescale whereas ![]() 's remain
independent. In the present paper we are going to check this
theoretical prediction numerically by directly measuring the
properties of
's remain
independent. In the present paper we are going to check this
theoretical prediction numerically by directly measuring the
properties of ![]() 's and
's and ![]() 's.
's.
In [6,4] RPA was assumed to hold over the nonlinear time. In [5] this assumption was examined a posteriori, i.e. based on the evolution equation for the multi-point PDF. Note that only the phase randomness is necessary for deriving this equation, whereas both the phase and the amplitude randomness are required for the WT closure for the one-point PDF or the kinetic equation for the spectrum. This fact allows to prove that, if valid initially, the RPA properties survive in the leading order in small nonlinearity and in the large-box limit [5]. Such an approximate leading-order RPA is sufficient for the WT closure.