


Next: Approximate independence of the
Up: Evolution of the multi-mode
Previous: Equation for
Taking the inverse Laplace transform of (35) we have the following
equation for the PDF,
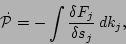 |
(35) |
where 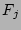 is a flux of probability in the space of the amplitude
is a flux of probability in the space of the amplitude 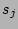 ,
,
This expression can be simplified to
This equation is identical to the one originally obtained
by Peierls [15] and later rediscovered
by Brout and Prigogine [16] in the context of
the physics of anharmonic crystals.
Zaslavski and Sagdeev [17] were the first to study this
equation in the WT context. However, the analysis of
[15,16,17]
was restricted
to the interaction Hamiltonians of the ``potential energy'' type,
i.e. the ones that involve only the coordinates but not the momenta.
This restriction leaves aside a great many important WT systems,
e.g. the capillary, Rossby, internal and MHD waves.
Our result above
indicates that the Peierls equation
is also valid in the most general case of 3-wave systems.
Here we should again emphasise importance of the taken order
of limits, 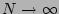 first and
first and
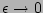 second.
Physically this means that the frequency resonance is broad
enough to cover great many modes. Some authors, e.g. [15,16,17],
leave the sum notation in the PDF equation even after the
second.
Physically this means that the frequency resonance is broad
enough to cover great many modes. Some authors, e.g. [15,16,17],
leave the sum notation in the PDF equation even after the
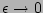 limit taken giving
limit taken giving
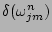 .
One has to be careful interpreting such formulae because
formally the RHS is nill in most of the cases because
there may be no exact resonances between the discrete
.
One has to be careful interpreting such formulae because
formally the RHS is nill in most of the cases because
there may be no exact resonances between the discrete  modes
(as it is the case, e.g. for the capillary waves). In real finite-size
physical systems, this condition means that the wave amplitudes, although
small, should not be too small so that the frequency broadening is sufficient
to allow the resonant interactions. Our
functional integral notation is meant to indicate that
the
modes
(as it is the case, e.g. for the capillary waves). In real finite-size
physical systems, this condition means that the wave amplitudes, although
small, should not be too small so that the frequency broadening is sufficient
to allow the resonant interactions. Our
functional integral notation is meant to indicate that
the 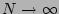 limit has already been taken.
limit has already been taken.



Next: Approximate independence of the
Up: Evolution of the multi-mode
Previous: Equation for
Dr Yuri V Lvov
2007-01-17
![$\displaystyle 4 \pi {\epsilon}^2 \int
\big\{
(\vert V_{mn}^{j}\vert^2 \delta(\o...
...ft[ s_n s_m {\cal P} - {\delta \over \delta s_j} (s_j s_n s_m {\cal P}) \right]$](img250.png)
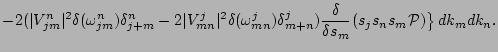
![]() first and
first and
![]() second.
Physically this means that the frequency resonance is broad
enough to cover great many modes. Some authors, e.g. [15,16,17],
leave the sum notation in the PDF equation even after the
second.
Physically this means that the frequency resonance is broad
enough to cover great many modes. Some authors, e.g. [15,16,17],
leave the sum notation in the PDF equation even after the
![]() limit taken giving
limit taken giving
![]() .
One has to be careful interpreting such formulae because
formally the RHS is nill in most of the cases because
there may be no exact resonances between the discrete
.
One has to be careful interpreting such formulae because
formally the RHS is nill in most of the cases because
there may be no exact resonances between the discrete ![]() modes
(as it is the case, e.g. for the capillary waves). In real finite-size
physical systems, this condition means that the wave amplitudes, although
small, should not be too small so that the frequency broadening is sufficient
to allow the resonant interactions. Our
functional integral notation is meant to indicate that
the
modes
(as it is the case, e.g. for the capillary waves). In real finite-size
physical systems, this condition means that the wave amplitudes, although
small, should not be too small so that the frequency broadening is sufficient
to allow the resonant interactions. Our
functional integral notation is meant to indicate that
the ![]() limit has already been taken.
limit has already been taken.