


Next: The order -
Up: text
Previous: Summary
Let us split 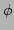 into its real and imaginary parts
into its real and imaginary parts
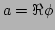 and
and
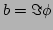 . Then the equation (
. Then the equation (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) splits into two
coupled equations
) splits into two
coupled equations
where we have used the fact that
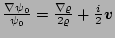 , which follows from
(
, which follows from
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ).
).
Gabor transforming our two coupled equations (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) and
(
) and
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ) and using Taylor series to represent large-scale
quantities,
) and using Taylor series to represent large-scale
quantities,
we find
Where
![$ {\cal G}[f(x)]$](img231.png) is the Gabor transform of
is the Gabor transform of 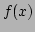 . We have kept
only
. We have kept
only
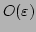 terms and neglected the
terms and neglected the
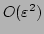 and
higher order terms. For generality, we have kept the nonlinear term.
and
higher order terms. For generality, we have kept the nonlinear term.
Subsections



Next: The order -
Up: text
Previous: Summary
Dr Yuri V Lvov
2007-01-23
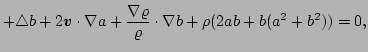
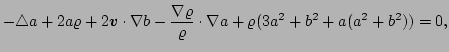
![]() ) and
(
) and
(![]() ) and using Taylor series to represent large-scale
quantities,
) and using Taylor series to represent large-scale
quantities,